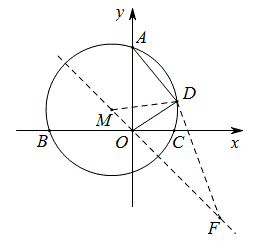又称阿波罗尼斯圆,已知平面上两点A、B,则所有满足PA/PB=k且不等于1的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆。
一、证明
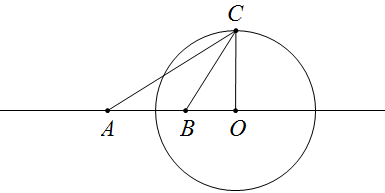
已知AB=p,点C是一个动点,常数k≠1,且满足CA:CB=k,求证点C的轨迹是一个圆。
证明1:坐标法
设点A(0,0),点B(p,0),点C(x,y),由\dfrac{\sqrt{x^2+y^2}}{\sqrt{(x-p)^2+y^2}}=k,变形后即得圆方程。
证明2:几何法
要使CA:CB=k,一定在直线AB上存在一点O,使△OCB∽△OAC,这时\dfrac{CA}{CB}=\dfrac{OC}{OB}=k,且OC^2=OB\times{OA},设OB=a,则OC=ka,
∴ka^2=a(a+p),a=\dfrac{p}{k^2-1},于是可以确定点O的位置,且OC为ka(常量),∴点C的轨迹是圆。
二、应用
例1 在△ABC中,角A,B,C的对边是a,b,c,c=2,b=2a,则三角形面积的最大值是 。
解:运用证明2的结论,由于p=2,k=2,∴a=\dfrac{2}{2^2-1}=\dfrac{2}{3},
∴圆的半径为\dfrac{4}{3},∴当OC⊥AB时,面积最大,S最大值=\dfrac{4}{3}。
三、阿氏圆的逆命题
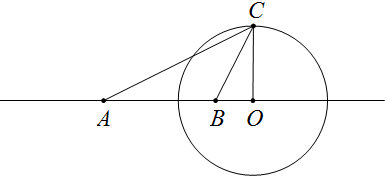
如上图,点B是定点,当点C在定圆O上运动时,必存在一个定点A,使得AC=kBC(k为常数,k≠1)始终成立。
说明:点A一定在直线OB上,且满足OC^2=OB\times{OA}。
四、逆命题的应用
例2 如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0)。过A,B,C作外接圆,D为圆上一个动点,求\sqrt{5}DO+DA的最小值。
解:易求圆心M(-1,1),在直线MO上取一点F,使F的坐标为(4,-4),则MD^2=MO\times{MF}。
所以△MOD∽△MDF,则当点D移动时DF=\sqrt{5}DO,
故\sqrt{5}DO+DA=AD+DF≥AF=4\sqrt{5}。