叶中豪提出了如下几何问题:
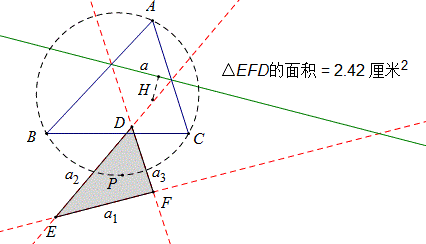
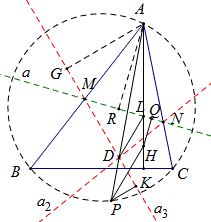
如图,H是△ABC的垂心,直线a是任意的一条直线,直线a_1、a_2、a_3是直线a关于BC、AC、AB轴对称直线。三条对称直线围成△DEF。
(1)何时D、E、F共点?实验发现直线a过H时共点。
(2)△DEF的面积由H到a的距离决定。
(3)△DEF的内心P在△ABC的外接圆上。
(4)当直线a位置变化时,△DEF的形状不变。
七中樊贞惠给出了如下的命题及解答。
命题1:
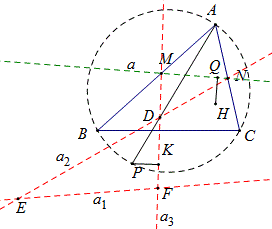
如图,⊙O是△ABC的外接圆,直线a_1、a_2、a_3是直线a关于BC,AC,AB轴对称直线,三条直线分别交于D、E、F,P是△DEF的内心.求证:P在⊙O上.
证明:在△DMN中,A是△DMN的旁心,
∴AD是∠MDN的角平分线,∴直线AD经过点P,且∠EDF=180°-2A.
同理可证,CE是∠DEF的角平分线,即直线CE经过点P,∠DEF=180°-2C.
∠DPC=90°-∠A+90°-∠C=∠B,∴点P在⊙O上.
顺便可得,∠DFE=180°-2B.
命题2
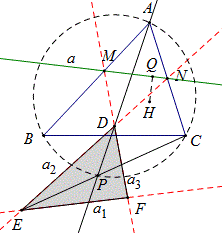
如图,⊙O是△ABC的外接圆,直线a、a_3关于AB对称,直线a、a_2关于AC对称,a_3、a_2交于点D,直线AD交⊙O于P,H是△ABC的垂心,a交AH于L. 求证:DL∥PH.
证明:作AG⊥a_3于G,设∠BMD=α,由上题可知,∠ADG=∠ADN=90°-A,
可证∠GAD=∠A,∴∠MAG=∠PAC=90°-α,
则∠ALM=180°-(α+90°-B)=90°-α+B=∠ABP.
在△ADM中,\dfrac{AD}{sin\alpha}=\dfrac{AM}{sin(90-A)},在△AML中,\dfrac{AL}{sin\alpha}=\dfrac{AM}{sin\angle{ALM}},
∴\dfrac{AL}{AD}=\dfrac{sin(90-A)}{sin\angle{ALM}},
在△ABH中,\dfrac{AB}{sinC}=\dfrac{AH}{sin(90-A)},在△ABP中,\dfrac{AB}{sinC}=\dfrac{AP}{sin\angle{ABP}},
∴\dfrac{AH}{AP}=\dfrac{sin(90-A)}{sin\angle{ABP}},
∴\dfrac{AL}{AD}=\dfrac{AH}{AP},∴DL∥PH.
命题3
如图,⊙O是△ABC的外接圆,直线a、a_3关于AB对称,直线a、a_2关于AC对称,a_3、a_2交于点D,直线AD交⊙O于P,H是△ABC的垂心,a交AH于L. HQ⊥a于Q,PK⊥a_3于K.求证:HQ=PK;HQ=DP·cosA.
证明:作AG⊥a_3于G,AR⊥a于R,可得\dfrac{HQ}{AR}=\dfrac{HL}{AL} ,\dfrac{PK}{AG}=\dfrac{DP}{AD},
由上题结论,\dfrac{HL}{AL}=\dfrac{DP}{AD} ,又∵AG=AR,∴PK=HQ,
又∵∠PDK=90°-A,∴HQ=DP·cosA.
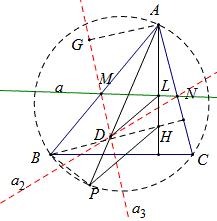
命题4
如图,⊙O是△ABC的外接圆,直线MN关于三边的对称直线分别交于D、E、F,H是△ABC的垂心,设HQ=h. 求证:S_{\triangle{D}{EF}}=(tanA+tanB+tanC)h^2.
证明:由命题1结论可知,P是△ABC的内心,HQ=PK=h,
∠EDF=180°-2A,∠DEF=180°-2C,∠DFE=180°-2B.
∴∠PDK=90-A,DK=\dfrac{PK}{tan(90-A)}=htanA,
同理,KF=htanB,∴DF=htanA+htanB,
同理,DE=htanA+htanC,EF=htanB+htanC,
所以
S_{\triangle{D}{EF}}=\frac{1}{2}(2htanA+2htanB+2htanC)h=(tanA+tanB+tanC)h^2.
于是当Q点在以H为圆心的圆上运动时,△DEF的面积和形状保持不变,即始终全等。
命题5
当直线a经过H时,直线a_1、a_2、a_3共点,当△ABC不变时,△DEF的形状也不变。
证明:当直线a经过H时,h=0,△DEF的内心P到三边的距离为0,即三线共点。
当△ABC不变时,△DEF的三个角大小也不变,所以△DEF的形状也不变。
黑马对老封的四个命题作了如下的解答:
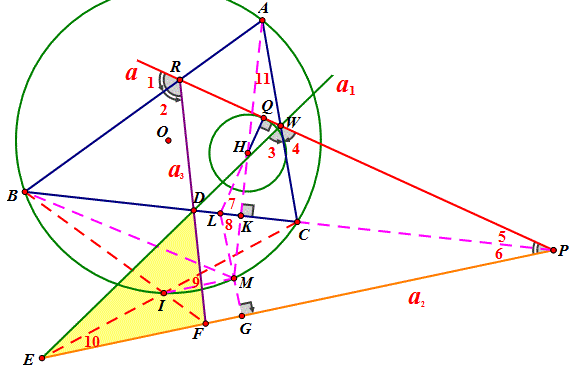
如图,(对锐角三角形情形进行证明)由题意得,∠1=∠2,∠3=∠4,∠5=∠6,∴点C是△WEP的内心,B是△PRF的旁心,D是△ARW的旁心,∴CE平分∠DEF,BF平分∠DFE, ∴I是△DEF的内心,且∠RFP=2∠B,∠EDF=180°-2∠A,∴∠DFE=180°-2∠B, ∠DEF=180°-2∠C,
∵∠BIC=∠EIF=90°+1/2(180°-2∠A)=180°-∠A, ∴点I在圆O上,(3)(4)获证.
连接AH交BC于K,交⊙O于M,延长QH交BC于L,连接LM并延长交EP于G
∵H为△ABC的垂心,∴HK=MK, ∴LH=LM, ∠7=∠8,∴LG⊥PE,∴LQ=LG,
∴MG=HQ,∵∠9=∠11=∠10=90°-∠C,∴IM∥EP,即△DEF内切圆半径为a,
∴S△DEF=1/2(DE+EF+DF)a=(tanA+tanB+tanC)a2. (1)(2)得证。