西姆松定理及其退化形式

一、西姆松定理及其证明

1、定理

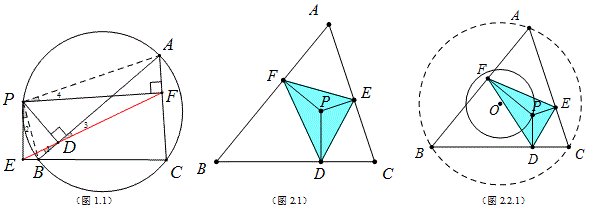
如图1.1，P是△ABC外接圆上一点，自P向三边所在的直线作垂线，垂足是D,E,F，那么D,E,F三点共线．

2、证明

连PA、PB，∵P、E、B、D及P、D、F、A四点共圆，
∴∠1=∠2，∠3=∠4，
∵∠AFP=∠BEP，∠FAP=∠EBP，∴∠2=∠4，
∴∠1=∠3，∴D、E、F三点共线．

二、西姆松定理退化1

1、结论1

当P点退化成不在外接圆上时，D,E,F三点构成三角形（如图2.1），而且这个三角形的形状可以任意改变．

2、结论1的验证

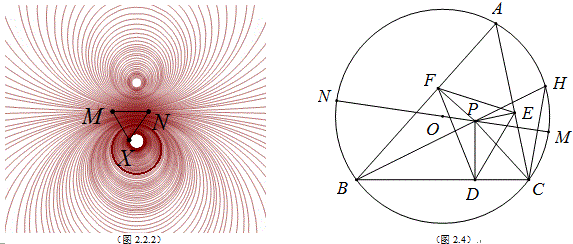
在几何画板中，画一边MN固定的△MNX，使△MNX∽△DEF，当P点在△ABC外接圆的同心圆上移动时（如图2.2.1），点X的轨迹是圆（记为圆Q），当同心圆的半径由小到大变化时，圆Q的跟踪是一族圆（如图2.2.2），并有两个空洞，上方的一个当OP=0时取得，下方的一个当OP=∞时取得．

这说明X在整个平面上可以到处跑，即△DEF的形状可以任意改变．

3、结论2

当P在△ABC外接圆的同心圆⊙O上移动时，△DEF的面积为一个定值（如图2.2.1）．

4、结论2的证明

如图2.4，△ABC为定三角形，O为外心，OP为定长，MN是过O,P的直径，设MN=2R，那么B,D,P,F四点共圆，BP为这个圆的直径， DF=BP·sinB（这里的∠B指的是∠ABC，∠C指的是∠ACB，下同），同理DE=CP·sinc.

△DEF的面积= $\frac{1}{2}$ DE·DF·sin∠EDF = $\frac{1}{2}$ BP·sinB·CP·sinC·sin∠EDF ，

易证∠EDF=∠PCH， $\dfrac{CP}{sinH}=\dfrac{PH}{sin\angle{PCH}}=\dfrac{CP}{sinA}$ ，

故△DEF的面积= $\frac{1}{2}$ BP·PH·sinA·sinB·sinC = $\frac{1}{2}$ │ $R^2-OP^2$ │sinA·sinB·sinC ，

这就说明当OP为定长时，△EDF的面积为定值．

三、西姆松定理退化2

1、结论3

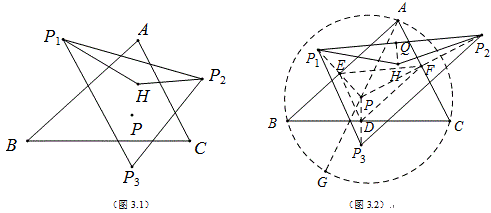
如图3.1，P是定△ABC所在平面内任意一点，P关于三边的对称点为 $P_1$ 、 $P_2$ 、 $P_3$ ，H是△ABC的垂心，当P点运动时，求证： $S_{{\triangle}HP_1P_2}:S_{{\triangle}P_1P_2P_3}$ 为定值．

2、结论3的证明

如图3.2，作HQ⊥P₁P₂于Q，连PP₁,PP₂,PP₃分别交三边于E,F,D，直线AP交△ABC外接圆O于G，那么

$S_{{\triangle}P_1P_2P_3}=4{\cdot}$ $S_{{\triangle}{D}{E}{F}}=2|{R^2-OP^2}|sinA{\cdot}sinB{\cdot}sinC$ ,

$S_{{\triangle}HP_1P_2}=\frac{1}{2}P_1P_2{\cdot}HQ=\frac{1}{2}{\cdot}2EF{\cdot}HQ$ ,

$=PA{\cdot}sinA{\cdot}PG{\cdot}cosA=|{R^2-OP^2}|{\cdot}sinA{\cdot}cosA$ ,

∴ $\dfrac{S_{{\triangle}HP_1P_2}}{S_{{\triangle}P_1P_2P_3}}=\dfrac{cosA}{2sinB{\cdot}sinC}$ ,

其中HQ=PG·cosA的证明过程比较冗长，这里限于篇幅不再累赘，在下一篇文章里写出．

3、结论4

从上面的证明可以得到如下推论：

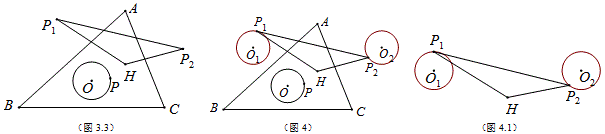
如图3.3，O、H分别为△ABC的外心和垂心，OP为定长，即P在△ABC外接圆的同心圆上，P关于AB、AC的轴对称点分别是P₁和P₂，那么 $S_{{\triangle}HP_1P_2}$ 为定值．

四、西姆松定理退化3

在结论4中，当P点沿着圆旋转时，P₁、P₂的轨迹是等圆O₁、O₂（如图4），并且当P点顺时针旋转时，P₁、P₂都是逆时针等速运动的．试想，如果事先给定的是两个等圆O₁、O₂，以及两圆上各一点P₁、P₂，当P₁、P₂同时逆时针等速运动时，是否可以在平面上确定一点H，使 $S_{{\triangle}HP_1P_2}$ 为定值？

1、结论5（结论4的逆命题）

如图4.1，给定两个等圆O₁、O₂，以及两圆上各一点P₁、P₂，当P₁、P₂同时逆时针等速运动时，在平面上存在一点H，使 $S_{{\triangle}HP_1P_2}$ 为定值．

2、结论5中H的作法

① 作O₁、O₂的中垂线；

② 设O₁O₂交两圆于M、N，P₁、P₂的起始位置分别为D、E，度量弧MD度数为α，弧NE的度数为β，计算γ=45+(β–α)÷4；

③ 作∠O₁O₂O=γ，交O₁O₂的中垂线于O；

④ 作△O₁O₂O的外心A；

⑤ 作A关于O₁O₂的对称点H．

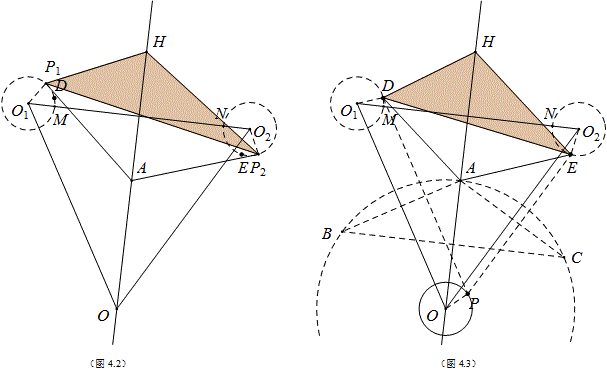
结论：点H即为所求（如图4.2）．

3、作法的证明

如图4.3，设P₁、P₂都处在起始位置D、E，以OA为半径作圆O，弦AB⊥O₁O，以AB为对称轴将圆O₁及D反射，D对应P，弦AC⊥O₂O，连EP．

∵∠POO₁=∠DO₁P=α+γ，

∴∠POO₂=∠POO₁-∠O₁O O₂=α+γ-(180-2γ)= α+3γ-180.

= $\alpha+3(45+\frac{\beta-\alpha}{4})-180=\frac{3}{4}\beta+\frac{1}{4}\alpha-45=\beta-\gamma$ .

∴四边形OPEO₂为等腰梯形，即E、P关于AC成轴对称．

易证，当P₁、P₂等速逆时针旋转时，它们关于AB、AC的对称点为小圆O上的同一点，

还可以证明，H是△ABC的垂心．

由结论4可知， $S_{{\triangle}HP_1P_2}$ 为定值．

五、拓展与猜想

1、在结论5的作图中，我们可以证明△P₁AP₂的形状不变．

2、是否可以将结论5中的等圆改为不等圆，等速改为等角速度，结果一样吗？