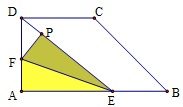
问题:如图,直角梯形纸片ABCD,AD⊥AB,AB=6,AD=CD=3,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P,当P落在直角梯形内部时,PD的最小值等于 。
要解决这个问题并不容易,用几何画板做一个课件吧。步骤如下:
(1) 画出满足条件的梯形ABCD;
(2) 在线段AB、AD上分别取点E、F;
(3) 以EF为对称轴反射点A至P,连PE,PF,PD;
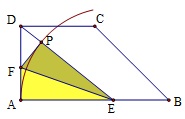
(4) 选中点F和点P,构造→轨迹;
(5) 拖动F点,发现D、P、E三点共线时,DP最小;
(6) 拖动E点,发现E和B重合时PD最小;
这样就得出一个结论:PD的最小值是BD-AB。其中步骤(5)的结论容易证明,但步骤(6)的结论如何证明呢?
下面的步骤更神奇:
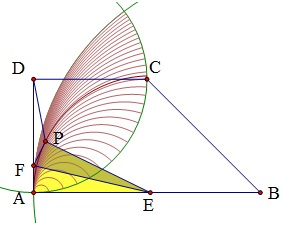
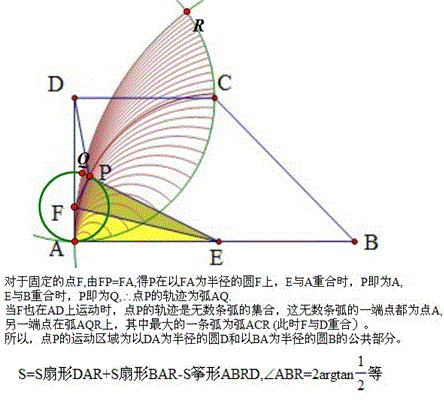
(7) 选中点E和轨迹,构造→曲线系,发现P点运动的区域是以D为圆心,AD为半径的圆和以B为圆心,AB为半径的圆的公共部分。
如何计算这个区域的面积呢?如何证明步骤(7)的结论呢?
亲,你能解决以上3个问题吗?
2013年9月10日追加:
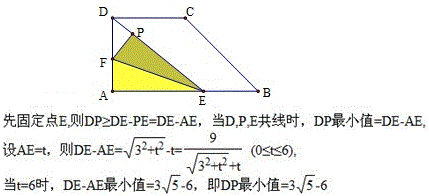
有位老师叫阿舒,他帮我做了解答如下: