在几何画板中画了一个三角形ABC和一条角平分线AD，拖动A点时发现：
当A点和BC的距离d保持不变时，D点的活动范围不是很大，而且d越大，D点的活动范围就越小。于是就猜想：D点的活动范围（设为m）是受d和BC的长a制约的。也就是说d和a可以表示m。
亲，你如果认为我的猜想是对的，请帮我解决写出这个关系式。
下面是三种解答方法：
在慈溪桥头李先兵老师的启发下，我试着解答如下：
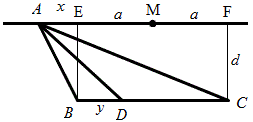如图，作矩EFCB，设BC=2a，EM=FM=a，BE=CF=d，AM=x，BD=y，
由角平分线定理得：\dfrac{AB}{AC}=\dfrac{BD}{CD}，即\dfrac{\sqrt{(a-x)^2+d^2}}{\sqrt{(a+x)^2+d^2}}=\dfrac{y}{2a-y}，
运用合比定理：\dfrac{y}{2a}=\dfrac{\sqrt{(a-x)^2+d^2}}{\sqrt{(a-x)^2+d^2}+\sqrt{(a+x)^2+d^2}}=\dfrac{1}{1+\frac{\sqrt{(a+x)^2+d^2}}{\sqrt{(a-x)^2+d^2}}}，
设\dfrac{\sqrt{(a+x)^2+d^2}}{\sqrt{(a-x)^2+d^2}}=\sqrt{t}，则y=\dfrac{2a}{1+\sqrt{t}}，
由上面的“设”，可得：(t-1)x^2-2a(t+1)x+(t-1)(a^2+d^2)=0
△=4a^2(t+1)^2-4(t-1)^2(a^2+d^2)≥0，
化简得：d^2t^2-(4a^2+2d^2)t+d^2≤0，得对应方程的两根为
t=\dfrac{2a^2+d^2\pm{2a}\sqrt{a^2+d^2}}{d^2}=\dfrac{(\sqrt{a^2+d^2}\pm{a})^2}{d^2}，
故y最大值=\dfrac{2a}{1+\sqrt{\frac{(\sqrt{a^2+d^2}-a)^2}{d^2}}}=\dfrac{2ad}{d+\sqrt{a^2+d^2}-a}=\sqrt{a^2+d^2}-d+a，
所以D点的活动范围m=2·y最大值-2a=2\sqrt{a^2+d^2}-2d。
从这个结果我们还可以解释d越大m就越小。
事实上，m=2\sqrt{a^2+d^2}-2d=\dfrac{4a^2}{2\sqrt{a^2+d^2}+2d}=\dfrac{2a^2}{\sqrt{a^2+d^2}+d}，
可见，m随着d的增大而减小。
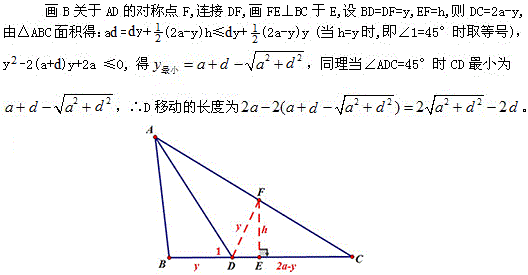
奉化奉港初中舒绍云老师提供了他的妙解，舒服啊。
至于大家猜想，当y取得最小值时，∠ADB=45°是否正确，回答是肯定的。
事实上，当∠ADB=45°时，x+y-a=d，
又y最小值=a+d-\sqrt{a^2+d^2}，可知x=\sqrt{a^2+d^2}，
故只要验证方程(t-1)x^2-2a(t+1)x+(t-1)(a^2+d^2)=0的解是不是x=\sqrt{a^2+d^2}，其中t=\dfrac{(\sqrt{a^2+d^2}+a)^2}{d^2}，
我们先将这个方程变形成x^2-2a\dfrac{t+1}{t-1}x+(a^2+d^2)=0,
这里\dfrac{t+1}{t-1}=\dfrac{a^2+d^2+a\sqrt{a^2+d^2}}{a^2+a\sqrt{a^2+d^2}}，代入后化简得：
x^2-2\sqrt{a^2+d^2}x+a^2+d^2=0，x=\sqrt{a^2+d^2}.
如何从几何角度解释这个奇妙的现象呢？
黑马解答如下：
以上三种方法都是代数研究问题，就算是第三种方法也没有用纯几何方法说明。亲，你如果有纯几何方法说明为什么45°时y达到最小值，请给出评论。
好啊