有许多数学问题,用函数图象解决优于其它方法, 而这恰恰是许多人想不到的。究其原因是缺乏函数思想和数形结合思想。
我相信,当你看完以下题目的解答后,一定会收到启发,利用函数图象解决问题的方法便会成为你有力的工具。
一、函数图象解决方程问题
例1 已知关于x的一元二次方程(x-1)(x-2)=m(m>0)的两个解分别是a和b,那么关于x的一元二次方程(x-a)(x-b)+m=0的两个解是什么?
解:构造三个函数如下:
y_1=(x-1)(x-2),y_2=(x-a)(x-b),y_3=(x-a)(x-b)+m,前两个函数图象如下:
由图可知,函数y_2=(x-a)(x-b)的图象可以看作是函数y_1=(x-1)(x-2)图象向下平移m个单位得到的。
再将函数y_2=(x-a)(x-b)的图象向上平移m个单位就得到y_3=(x-a)(x-b)+m,也就是y_1=(x-1)(x-2),
所以一元二次方程(x-a)(x-b)+m=0的解就是(x-1)(x-2)=0 的解,即解为x_1=1,x_2=2.
例2 设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α、β(α<β),则α、β满足( )
A、1<α<β<2 B、1<α<2<β C、α<1<β<2 D、α<1且β>2
解:构造函数y=(x-1)(x-2),并画出其图象作直线y=m,发现D是对的。
例3 已知关于x的方程-x^2+ax+1=0的一个根大于1而小于2,求a的取值范围。
解:先画出符合条件的函数图象:
由图可知,f(1)>0,f(2)<0,即\begin{cases} -1+a+1>0\\ -4+2a+1<0 \end{cases}
所以0<x<\frac{3}{2}
二、函数图象解决函数问题
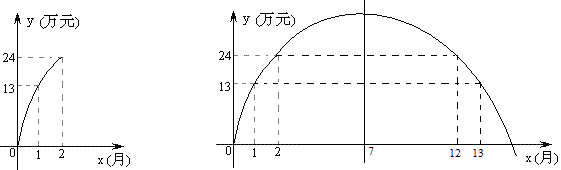
例4 一家电脑公司推出一款新型电脑,投放市场以来,前两个月的利润情况如图所示,该图可以近似地看作抛物线的一部分,其中第x月的利润为y万元,往后y与x满足的关系不变.请结合图象解答下列问题:
公司打算,从月利润下降开始,若后一个月与前一个月利润之差超过11万元,就停止销售该产品,请你预测该产品持续销售的时间.
解:如上右图,根据抛物线的对称性可知,第12月到13月利润刚好下降11万元,所以持续销售时间是13个月。
例5 如图,抛物线y=2x^2-\frac{5}{2}x+a与x轴正半轴交于A、B两点(A在B的左边),与y轴正半轴交于C,且∠OCA=∠OBC,则B点坐标是 ( )
A、(\frac{1}{4},0) B、(4,0) C、(1,0) D、(3\sqrt{3},0)
解:如右图,画出抛物线的对称轴,利用图象的对称性来解。
此抛物线的对称轴是直线x=\frac{5}{8},如图,利用对称性知,B点的横坐标介于\frac{5}{8}和\frac{5}{4}之间,只有C符合。
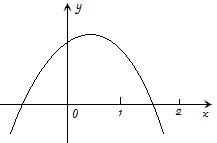
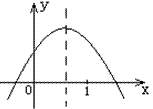
例6 已知二次函数y=ax^2+bx+c的图象如图所示,试判别代数式a+b的符号。
解:a+b=(a+b+c)-c=f(1)-f(0),从图象中可见,x=1的函数值比x=0时函数值大,所以a+b>0.
例7 若二次函数y=ax^2+bx+c(a\neq{0}的图象过点(0,1)和(–1,0)且顶点在第一象限,则S=a+b+c的值的变化范围是 ( )
A、0<S <1 B、0 <S <2 C、1 <S <2 D、–1< S< 2
利用函数图象的解法:
S = a + b + c是x=1时函数的值,从图象的变化可以看出,函数y=-x^2+1和y=x+1是变化过程中的两个极端位置,所以,S的值介于0与2之间,所以选B.
三、函数图象解决不等式问题
例8 已知直线y=kx+b过点A(0,2),且与直线y=mx交于点P(1,m),则不等式mx>kx+b>mx-2的解是 。
分析:用代数方法虽然也可以解决,但甚繁。如果画出如下的图形,就一目了然了。
结果是1<x<2.
例9 已知当x为正数时,不等式ax^2-2x+1>0恒成立,求a的取值范围。
解:如果利用二次函数问题考虑,会发现满足条件的二次函数图形情况很多,不利于解决问题。
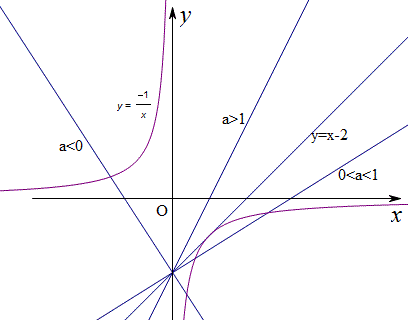
如果将函数化为ax-2>-\dfrac{1}{x}再考虑,会画出如下的图象:
我们看到a=1或a=0是两个极端位置,所以当a>1或a<0时ax-2>-\dfrac{1}{x}恒成立。
四、函数图象解决其它问题
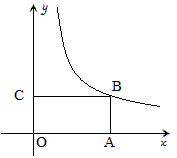
例10 如图,矩形OABC中,O是坐标原点,A,C在坐标轴上,B在双曲线y=\dfrac{12}{x}上,用尺规作OA,OC的比例中项。
解:作∠AOC的角平分线,交双曲线于D,过D作x轴垂线DE,垂足为E,那么DE即为所求的线段。
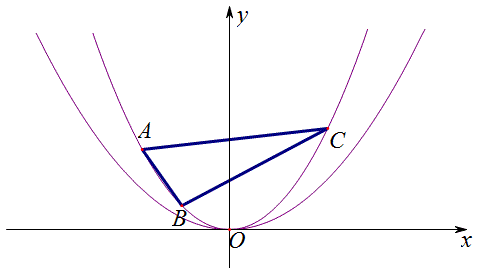
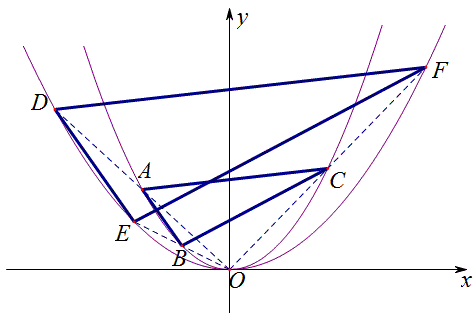
例11 如图,抛物线y=ax^2和抛物线y=bx^2(b<a)在同一坐标系中,A,B,C三点在抛物线y=ax^2上,请只用直尺画一个△DEF,使△DEF∽△ABC,且\dfrac{S_{\triangle{ABC}}}{S_{\triangle{{D}EF}}}=\dfrac{b^2}{a^2}.
解:如下图△DEF即为所求的三角形。
证明:过A,D作x轴的垂线,垂足是A’和D’,那么△AA’O△DD’O,所以\dfrac{OA}{OD}=\dfrac{OA'}{OD'}=\dfrac{AA'}{DD'},设A,D的横坐标分别为m、n,即\dfrac{OA}{OD}=\dfrac{m}{n}=\dfrac{am^2}{bn^2},
故\dfrac{m}{n}=\dfrac{b}{a}=\dfrac{OA}{OD},同理\dfrac{OA}{OD}=\dfrac{OB}{OE}=\dfrac{OC}{OF}=\dfrac{b}{a},
所以,由位似知识可得△DEF∽△ABC,且\dfrac{S_{\triangle{ABC}}}{S_{\triangle{{D}EF}}}=\dfrac{b^2}{a^2}.
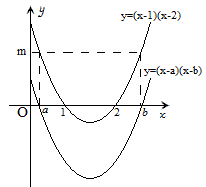
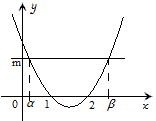
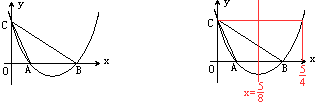

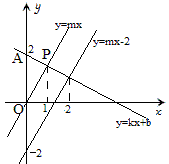
你说得对,我疏忽了,谢谢你。
黄老师,例9的a取值范围a小于0,我看不可以,因为X大于直线与双曲线的交点的横坐标时,反比例大于直线。