学生练习中有一道二次函数应用题:
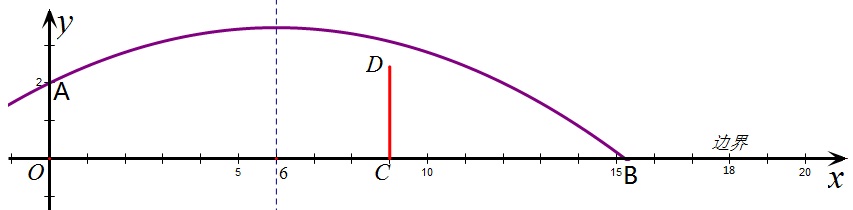
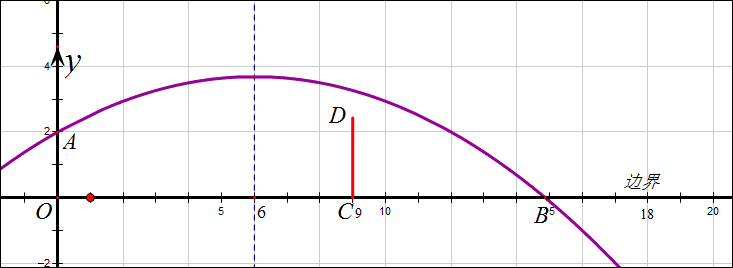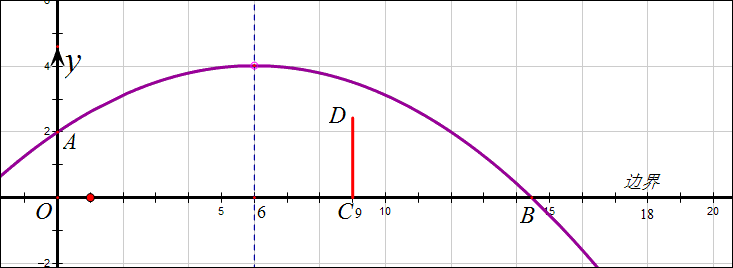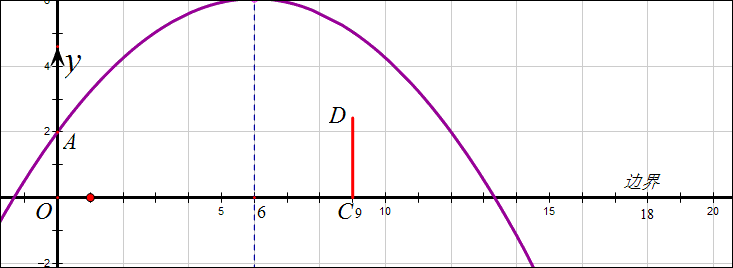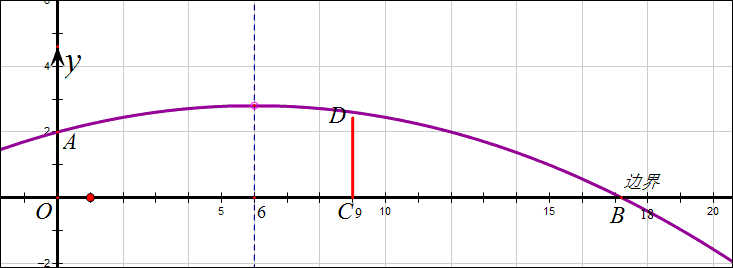
(安徽2012年)23.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)^2+h.已知球网CD与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。
本题有3个小题,前2个小题略。
我做第(3)题的方法是采用极端原理。
解:当抛物线过D点时,可以将A(0,2)及D(9,2.43)代入,得
\begin{cases} 36a+h=2\\ 9a+h=2.43 \end{cases},解得\begin{cases} a=-\frac{43}{2700}\\ h=\frac{193}{75} \end{cases},
当抛物线过边界(18,0)时,可以将A(0,2)及B(18,0)代入,得
\begin{cases} 36a+h=2\\ 144a+h=0 \end{cases},解得\begin{cases} a=-\frac{1}{54}\\ h=\frac{8}{3} \end{cases},
因为\frac{8}{3}>\frac{193}{75},所以\frac{193}{75}\le{h}\le\frac{8}{3}.
以上解答似乎没有问题,课堂上我就是这样讲的。但课后一位同学(陶心)给我看了他的解法:
由抛物线过A(0,2)得36a+h=2,即a=\frac{1}{18}-\frac{1}{36}h,
要不出界,当x=18时y<0,即144a+h≤0,将a代入得8-3h≤0,h\ge\frac{8}{3},
又要越过球网,所以当x=9时y≥2.43,即9a+h≥2.43,将a代入得\frac{1}{2}-\frac{1}{4}h+h\ge2.43,
h\ge\frac{193}{75},因为\frac{8}{3}>\frac{193}{75},所以h\ge\frac{8}{3}.
学生的结果与我完全相反!谁错了呢?
下图告诉我们,h越大球的落地点越靠近(12,0)(抛物线始终过(12,2)),落点B在(18,0)时h=\frac{8}{3},如果h\le\frac{8}{3}球将出界,所以必须是h\ge\frac{8}{3}.
事实上,当抛物线过D点时h=\frac{193}{75},此时球已经出界了,球只要不出界,则一定过球网。所以\frac{193}{75}\le{h}\le\frac{8}{3}这个范围是使球落在边界到出界的一段范围。
可见,学生的解答对了,我错了!
又有一天,学生作业里有一道题:
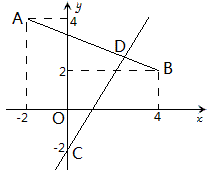
如图,在平面直角坐标系中线段AB的端点为A(-2,4),B(4,2),一直线y=kx-2与线段AB有交点,则k的值不可能是( )
A.-5 B.-2 C.3 D.5
当D与A重合时k=-3,当D与B重合时k=1,所以-3<k<1,所以选择A,C,D都对。
而事实上,D在AB上时,k<-3或k>1,只能选B。
由此,我们有如下结论:极端原理是不可靠的,因为极端原理只是求出了两个极端位置的值,取值范围不一定是这两个值之间,还得从实际情况考虑。
同学你弄错了,极端原理的确不适合用在此题中,因为在答卷中,时间有限,难以去解释为什么球在界内就一定会过网,而能保证过网不一定能保证落在界内。所以建议用陶心同学的方式。
其实不是极端原理用错了,是最后一步结论弄反了。所以说极端原理还是可行的