关于x的二次函数y=ax^2+bx+c图象如图所示。
(1)判断c-4b的符号;(2)判断a-2b+4c的符号;(3)如果OA=OB,求证:0<a<1.
解(1)
由\frac{b}{-2a}>1,得b<-2a,即-2b>4a,
∴c-4b=-2b-2b+c>4a-2b+c=f(-2)>0.
(2)
a-2b+4c=4(\frac{1}{4}a-\frac{1}{2}b+c)=4f(-\frac{1}{2})<0.
(3)
∵OA=OB,B点坐标为(0,c),∴A点坐标为(c,0),
∴ac^2+bc+c=0,ac+b+1=0,
∵f(1)<0,即a+b+c<0,∴b<-a-c,
∴ac-a-c+1>0,即(a-1)(c-1)>0,
∵c-1<0,∴a-1<0,即0<a<1.
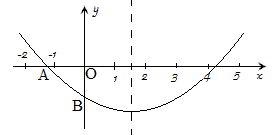
这位老师,你可能复制、粘贴了文章里的代码标签,所以不能显示。这个标签[latex]一定要自己手动输入的,我将你的内容稍作修改如下:
我利用你介绍的LaTex语法写写看,能不能成功。由ac+b+1=0知,a=[latex](-b-1)\div{c}=-b\div{c}-1\div{c}[/latex],又由(1)c>4b,所以[latex]-b\div{c}<-1\div{4}[/latex],由图-2
我的评论怎么不显示
我利用你介绍的LaTex语法写写看,能不能成功。由ac+b+1=0知,a=[latex](-b-1)\div{c}=-b\div{c}-1\div{c}[/latex],又由(1)c>4b,所以[latex]-b\div{c}<-1\div{4}[/latex],由图-2<c<-1,故0<[latex]-1\div{c}[/latex]<1,所以,a<[latex]-1\div{4}-1\div{c}<-1\div{4}+1=3\div{4}[/latex]<1。我把范围再次缩小,不知对否?(用LaTex语法不知能否成功?)
黄老师,今天听了你的几何画板培训,对我帮助很大,谢谢!看了你的博客又让我收获很多,再次谢谢!你出的这道题目很有意思,我做了一下不知道对不对,不知你去年的悬赏还有没有效??? —哈开玩笑呢!
学习到了,谢谢!
黄老师水平太高了,望尘莫及啊!我做了好久也没做全,学习到了,谢谢!