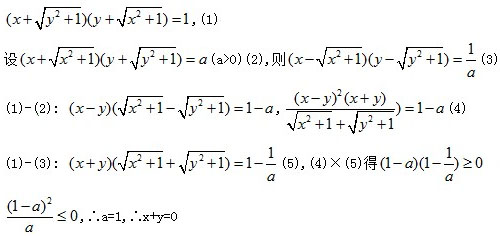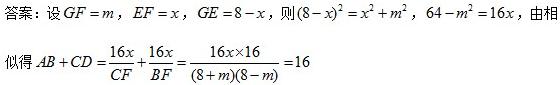《出众树雪》高手如林,展示的问题难度较高,解法让人叫绝,故拾圣人之遗,以飨读者。前面已经有3篇总汇:
问题30
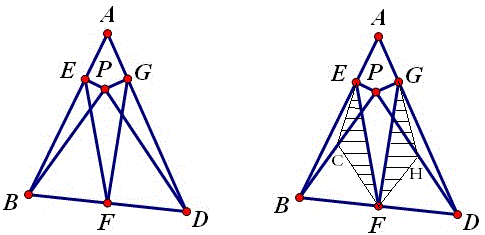
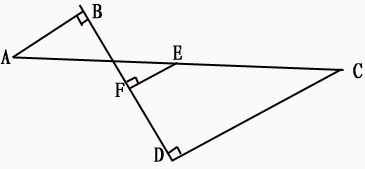
已知:如图P是△ABD内一点且∠ABP=∠ADP,PE⊥AB于E, PG⊥AD于G,F是BD中点,求证:EF=FG。(流星提供)
黑马解答:取PB,PD的中点C,H,则CF=HG=\frac{1}{2}PD,HF=CE=\frac{1}{2}PB,
∠ECP=2∠ABP,∠PCF=180°-∠BPD=∠PHF,∠GHP=2∠ADP,∴∠ECF=∠GHF,∴△ECF≌△GHF,故EF=FG.
樊贞慧解答:
如图,延长EF至H,使FH=EF,连结CH,EG,则可以证明EB=CH,∠EBC=∠3,∠GCH=180°-∠A=∠EPG,
由△PEB∽△PGC,得EP:GP=EB:GC=CH:CG,故△EPG∽△HCG,∴∠1=∠2,∴∠EGH=∠PGC=90°,
故GF是Rt△EGH斜边上的中线,故EF=GF。
问题31
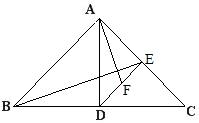
如图,△ABC中,AB=AC,D是BC的中点,DE⊥AC于E。F是DE的中点,求证:AF⊥BE。(成都罗老师提供)
黑马解:
先证三角形ADE相似三角形DCE,再证出三角形ADF相似三角形BCE。
问题32
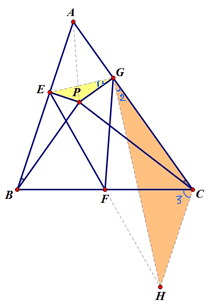
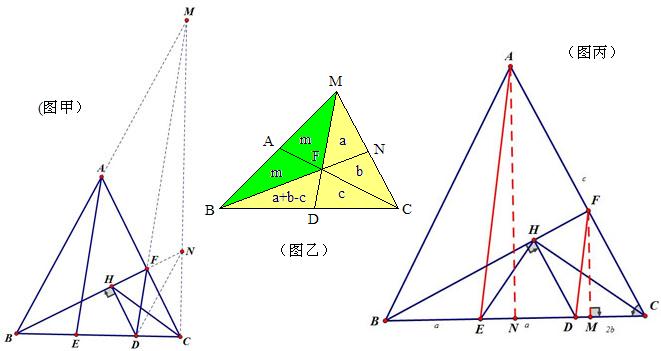
已知:AB=AC,BE=ED,AE//DF,DH⊥BF,求证:∠FHC=∠ACB.(黑马提供)
樊贞慧解:如图甲,延长BA和DF交于M,延长BF交MC于N,连结DN,则易证AM=AB,MC⊥BC,H,D,C,N共圆,∴∠FHC=∠NDC,只要证明ND∥MB即可。
但樊老师没有说明如何证明ND∥MB,经同行提示知道是用塞瓦定理证明的。
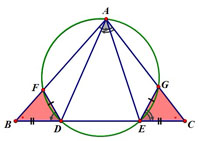
如图乙,F为△MBC内一点,由塞瓦定理:\frac{BD}{DC}\times\frac{CN}{MN}\times\frac{MA}{AB}=1,
∵AM=AB,∴\frac{BD}{DC}=\frac{MN}{NC},∴ND∥MB。
后来我用面积法又找到了一种证明ND∥MB的方法:
如图乙,设S△ABF=S△AMF=m,S△MNF=a,S△NFC=b,S△DCF=c,S△BDF=a+b-c,
则有\frac{b}{a}=\frac{a+b}{2m}=\frac{c}{a+b-c},
即\frac{CN}{MN}=\frac{CD}{BD},∴ND∥MB。
黑马的解法:如图丙,设AE=ED=a,DC=2b,
问题33
已知∠1=∠2,BD=CE,求证:AB=AC。
黑马一口气提出了如下6种方法:
方法1:
如图,作DM⊥AB于E,EN⊥AC于N,假如AB>AC,那么∠B<∠C,
∴∠ADE<∠AED,∴AD>AE,①
另一方面,∵△BDM和△CEN中,BD=CE,∠B<∠C,∴MD<NE,
故△ADM∽△AEN,AD<AE,②
①②是矛盾的,同理可证AB<AC也会矛盾,∴AB=AC。
方法2:作△ABC的外接圆,AD、AE的延长线交圆于F、G,
则由∠1=∠2可证EF=CG,∠FBD=∠GCE,∴△FBD≌△CGE,
∴∠F=∠G,∴AB=AC。
方法3:∵\frac{AD}{sinB}=\frac{BD}{sin\angle1}=\frac{EC}{sin\angle2}=\frac{AE}{sinC},∴\frac{AE}{sinB}=\frac{AD}{sinC},相除得AD=AE,就可以证明全等.
方法4:AB×AE=AD×AC,AB×AD=AE×AC(面积相等得出的),相乘得AB=AC。
方法5:如图作△ADE的外接圆,则∠FDB=∠BAE,∠GEC=∠DAG,
∵∠1=∠2,∴∠BAE=∠DAC,∴∠FDB=∠GEC,于是易证△BDF≌△CEG,
∴∠B=∠C,∴AB=AC。
方法6:如图,分别作△ABD和△ACE的外接圆,延长BA,CA交圆于N,M,先证明△MBD和△NEF全等,再证明△MBC和△NCB全等。
问题34(黑马提供)
洪利芳解答:
黑马有以下2种解法:
解法1
解法2
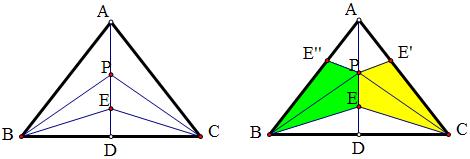
问题35
洪利芳提供:如图,在△ABC中,BE、BP三等分∠ABC,CE、CP三等分∠ACB,A、P、E共线,求∠BPE度数。(是《尖子生》中的题,答案是45°)
经几何画板操作发现,符合条件的三角形一定是等腰三角形,AD一定是顶角平分线。只要AB=AC均满足条件,那么∠BPE度数是变量了,∴这个问题无解。
接下来的问题:如何证明AB=AC、AD平分角BAC呢?
樊贞慧老师的证明:
如图,易证E是△BPC的内心,作△PBE和△PCE分别关于PB,PC的轴对称三角形,易证△AE’P≌△AE”P,故AD平分角BAC。AB=AC的证明就不难了。
问题36
黄冈朱老师提供:
黑马解:由面积法得3x+4y+5z=12,与\frac{3}{x}+\frac{4}{y}+\frac{5}{z}=12相加并配方得(\sqrt{3x}+\sqrt{\frac{3}{x}})^2+(\sqrt{4y}+\sqrt{\frac{4}{y}})^2+(\sqrt{5z}+\sqrt{\frac{5}{z}})^2=0,所以x=y=z=1,则结果为3.
问题37
张阿水提供:
黑马解答:
第(1)题是第(2)题的特例,(2)的解答如下:
问题38
如图,AB=AC=BD=CE,AD=BE,求∠ACE的度数。
解:作△BFE≌△ABD,那么BF∥AC,BF=AC,∴四边形ABFC是平行四边形。
故CF=AB,∴△CEF是正三角形。设∠1=x,那么∠A=180-x-60=120-x,
∠2=180-2(120-x)=2x-60=∠3,∵∠A=∠3+∠4,∴120-x=2x,x=40。
问题39
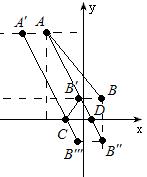
已知A(-4,8),B(2,2),C(-2,0),点A,B向x轴负方向平移相同的距离,设像为A’,B’,当A’C+B’C最小时,求A’的坐标。
解:如图设B关于x轴对称点为B”,AB”交x轴于D,将AB”平移使其过C点,得线段A’B”’,
这时A’C+B’C=A’B”’,两点之间线段最短。
易得线段AB”的解析式为y=-\frac{5}{3}x+\frac{4}{3}
∴D(\frac{4}{5},0),DC=\frac{4}{5}+2=\frac{14}{5},∴A'(-\frac{34}{5},8)
问题40
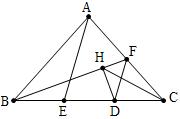
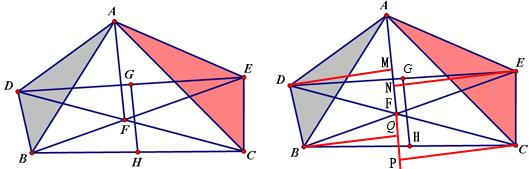
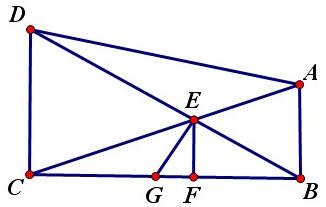
(水六杯提供)如图,△ADB∽△AEC(A对应A,D对应E),DC、BE交于E,G、H分别是DE、BC的中点,求证:GH∥AF。
证明(成都罗老师提供)
由相似可得\frac{1}{2}AD\times{AC}=\frac{1}{2}AB\times{AE},
即S△ADC=S△ABE,这说明 C,D到AF距离之和等于B,E到AF距离之和,
即DM+CP=BQ+EN,或EN-DM=CP-BQ.
如上图,当E是AC中点时,EF=\frac{1}{2}(DC-AB).
故在原图中有G,H到AF距离相等,这说明GH∥AF。
问题41
在直角梯形ABCD中,EF⊥BC,G为BC中点,BC=16,EG+EF=8,求AB+CD的值。
黑马解答: