定理:直角三角形斜边上的中线等于斜边的一半。
已知:如图Rt△ABC中,∠ACB=90°,D是AB的中点,求证:CD=\frac{1}{2}AB.
方法1:书本中的方法
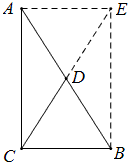
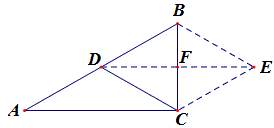
延长CD至E,使DE=CD,连AE、BE,
容易证明四边形ACBE是矩形,
∴CD=\frac{1}{2}CE=\frac{1}{2}AB.
方法2:
延长CD至E,使DE=CD,连AE,或者绕D点将△CDB旋转180°得△EDA,
容易证明△ACB≌△CAE,
∴CD=\frac{1}{2}CE=\frac{1}{2}AB.
方法3:
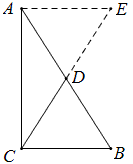
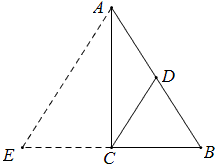
将△ABC沿AC反射得△ACE,∵∠ACB=90°,∴E,C,B三点共线,
∵D是AB的中点,C是EB中点,∴CD=\frac{1}{2}AE=\frac{1}{2}AB.
方法4:
作△ABC的中位线DE,那么DE∥BC,∵∠ACB=90°,∴DE⊥AC,
∴CD=AD=\frac{1}{2}AB.
方法5:
作△ABC的中位线EF,连ED、DF,
容易证明四边形CEDF是矩形,∴CD=EF=\frac{1}{2}AB.
方法6:同一法
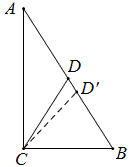
在AB上取一点D’,使D’C=D’B,∴∠D’CB=∠B,
∵∠A+∠B=90°,∠D’CA+∠D’CB=90°,∴∠A=∠D’CA,
∴AD’=CD’,故AD’=BD’,即D’是AB的中点。
又∵D是AB的中点,∴D’和D重合,∴CD=\frac{1}{2}AB.
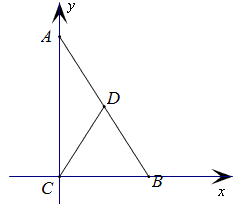
方法7:坐标法
如图,以C为坐标原点,直线CB为x轴建立坐标系。
设A点坐标是(0,a),B点坐标是(b,0),那么中点D的坐标是(\frac{b}{2},\frac{a}{2}),
所以AB=\sqrt{a^2+b^2},CD=\sqrt{(\frac{a}{2})^2+(\frac{b}{2})^2}=\frac{1}{2}\sqrt{a^2+b^2},
∴CD=\frac{1}{2}AB.
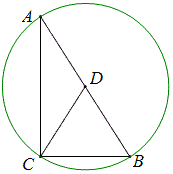
方法8:辅助圆法
作△ABC的外接圆,那么D是圆心,所以CD=\frac{1}{2}AB.
方法9:
如图,将△DBC沿BC反射得△EBC,那么 DE⊥BC,∵BC⊥AC,∴DE∥AC,
∵D是AB中点,∴E是BC中点,∴四边形DCEB是菱形,∴CD=DB,
所以CD=\frac{1}{2}AB.
方法10:反证法
假如CD≠AD,不妨设CD>AD,那么我们可以在CD上取一点E,使ED=AD=DB,于是∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,∴∠2+∠3=90°,
∵又∠2+∠3>∠ACB=90°,这是矛盾的(自相矛盾)
∴CD=\frac{1}{2}AB.
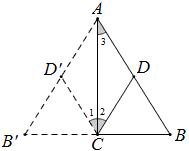
方法11:
将整个图形沿AC反射,可得CD’∥AB,∴∠1=∠3,∠1=∠2。
∴∠2=∠3,∴CD=AD=\frac{1}{2}AB.


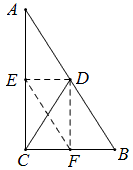

大开眼界!黄老师,您是如何想到这么多方法的?