课堂教学中一定会有一些事先不曾想到的结果发生,每一个人对数学教学的理解是各不相同的,可贵的是抓住每次难得的机会,不管是课堂里发生的还是事后想到的,如果不加记录整理,实在有点可惜。以前我要当同类问题积累到一定数量后才会写进博客,但后来发现这有一定难度,同类问题的数量不是很多,除非等待较长时间且不会遗忘。现在想想为何要同类呢?只要有新意的、可思考的、供讨论的、有感而发的、有价值的东西都可以及时记录。
问题1:三视图确定的几何体是否唯一确定?
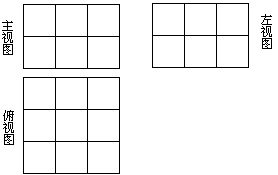
一直来都认为三视图确定的几何体是唯一确定的。所以工厂里靠三视图加工机器零件,动漫创作员靠三视图画出一辆汽车。可是有一天,课题是《由三视图描述几何体》,经过师生一起讨论,发现如下的三视图的几何体不唯一的。
所对应的几何体有很多,举例如下:
问题2:只有2个视图的几何体是否一定不唯一?
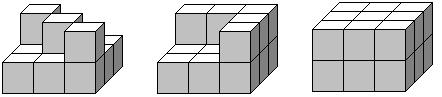
原以为只有2个视图的几何体不唯一,可后来发现不一定的,如下2个视图的几何体(由若干个相同的小正方体搭成)是唯一的:
问题3:两个相似的矩形,当对应边平行时,一定位似吗?
位似虽然不作要求了,但位似的内容确实可以引发很多思考。一次在讲解位似的题目时,发现相似的矩形,当对应边平行时,一定位似。
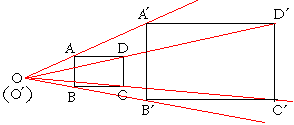
如图矩形ABCD∽矩形A’B’C’D’,AB∥A’B’,求证:直线AA’,BB’,CC’,DD’交于同一点。
设AA’.BB’交于O,AA’,DD’交于O’,则由相似三角形可以证明O,O’重合,同理可以证第四线也交于这点。
问题4:学生的作业、考卷教师是否要提前做一遍?
以前我是认真地做一遍后再给学生布置作业和考试的,初三复习讲解例题、习题前也这样。后来慢慢地省略这个做法,这是近6年的事。我发现光这一项,每天为自己省下好多时间,事先自己不做题,会有什么问题吗?答曰:利大于弊。
1、事先不解题,当场在学生面前分析、解答,学生看到的是人的真实想法,现场解答时老师会将思考的原始过程一览无余暴露于学生面前,其中还会有思路的偏差、矫正、方法的选择、辅助方法等等的思维特征体现,是学生活的教材。
2、不用担心临时解不出题,不用担心在学生面前出丑,这样反而和学生的距离拉近了。如果有学生自告奋勇解了老师解不出的题,那这个学生一定会感到光荣和自豪,成就感油然而生。
3、不用担心错误的题出现在作业中,这样反而可以锻炼学生判别是非的能力,鉴别错误的能力是必不可少的。
4、唯一的弊端是一些不合适的题出现在作业和试卷中,增加学生的无畏困难。不过这也不是大事。其一,现在试卷和作业本的质量比以前大有提高,不合适的题越来越少见。其二,反正现在的学生一见难题就会放手,也不碍事。其三,少数成绩好的学生会因这样的题耽误点时间,这也无妨,好的学生就需要锻炼嘛。
问题5:教师不备课就是失职吗?
如果一位教师已经能做到以下几点,那么他完全可以不备课。
1、对教材内容了如指掌;
2、能很好地把控教材,及时发现教材中的问题,能灵活地处理教材,能清楚地知道每节课的重、难点,也就是会用教材教,而不是教教材;
3、能清楚了解每一知识点在中考中的要求;
4、能当即编题,不需要任何参考;
5、能当即设计正对任何教学目的的问题和背景,能及时组织材料,发掘题目的多种功用。
6、解题达到一定水平,有许多解题方法和个人独特的经验,能从解一道题的方法归纳出解一类题的方法,能从数学思想的高度去分析解决问题。
不备课还有很多好处,最大的好处是上课随机应变,因人施教,不受条条框框约束,充分发挥教师个人特长,更容易把握重点和突破难点,更有利于提高教学质量。
问题6:二次根式第一节课能深化吗?
浙教版八下1.1二次根式,是一节内容空洞、难度极低的课。如何深化?如何不让学生因难度太低而乏味呢?我是这样进行的:
先讲好书上的内容,再做书上的“做一做”和“作业题”的第一题,全都是极其简单的求二次根式中字母的取值范围。学生没劲了,我说:咱们来点难题如何?
1、请你写出一个用x表示的代数式,使x不能取任何一个实数。
有学生写的是:\sqrt{\frac{1}{0\times{x}}}、\sqrt{\frac{1}{x-x}}
我马上补充:被开方数不要出现分式。许久有人写出\sqrt{-x^2},马上被大家否定了,马上有人得出\sqrt{-x^2-1}
2、请你写出一个用x表示的代数式,使x只能取唯一一个实数。
马上有学生写出:\sqrt{-\mid{x}\mid}和\sqrt{-x^2},
我再变化:被开方数不要出现绝对值,能否写一个x只能取1的代数式?
许久,有人写出\sqrt{-(x-1)^2}
我又规定:被开方数不能有绝对值、只能是一次式。这次都没辙了,很久都写不出来。我只好给出答案:\sqrt{x-1}+\sqrt{1-x},学生看了这个代数式大叫:太神奇了,比1大这个不行了,比1小那个不行了,真想不到。
3、已知实数x、y满足y=\sqrt{x-1}+\sqrt{1-x}-5,求x+y的值。
已是水到渠成之时,不费吹灰之力,一蹴而就。
问题7:灌输式好还是启发式好?
这要看具体问题而定。大多数的教学内容可以也应该用启发式教学,但不能否认灌输式在教学中的作用。早至孔子,灌输式以其较好的可操作性和有效性得到广泛的应用,并且一直沿用至今。我想,以下几种情况可以采用灌输式教学。
1、概念性很强,人为规定的因素很大。如有理数的乘法法则、圆的基本概念等。
2、很难启发、探索。如勾股定理、三角函数概念等。
3、启发、探索的价值不大。如平面直角坐标系等。
4、学生基础太差。
问题8:梯子滑动
初二上期末复习的试卷有这样一道题:
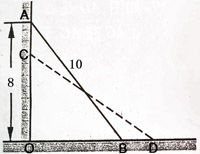
如图,长为10米的梯子斜靠在墙上,梯子顶端A距地面AO=8米,如果梯子顶端下滑2米到CD位置,那么梯子底端B向外滑动的距离BD是多少米?
答案:2米。
讲完解法后,我对同学们说:老师猜想梯子顶端下滑的距离是否等于底端外滑的距离?
这时学生纷纷说:应该对吧。
我叫同学们计算当AC=1时BD等于多少?大家很快算出BD≈1.1414,结果令大家失望,原来猜想错了。
接着我叫学生自己提出猜想或别的想法。
学生甲:我猜想AC和BD成比例。
大家想办法来证实这个猜想,许久学生甲自己推翻了猜想:我发现当AC=2时AC:BD=1,当AC=1时AC:BD<1,可见不成比例。
学生乙:我猜想AC与BD的大小关系以2为界,当AC=2时AC:BD=1,当AC<2时AC:BD<1,当AC>2时AC:BD>1.
大家又计算了当AC=3时BD≈2.66,AC:BD>1,
当大家再也提不出猜想时,我又抛出了一个想法:当梯子顶端匀速下滑时,底端外滑的速度是匀速、加速还是减速?
这时教室虽然很寂静,但学生分明投入到积极的计算中,一个学生的草稿被我展示出来:
| AC的长 | 1 | 2 | 3 |
| BD的长 | 1.1414 | 2 | 2.66 |
这时大家不难发现,底端外滑的速度是减速的。