《出众树雪》是一个小小的初中数学群,群号:88730268,2009年创办这个群,旨在群员之间互相研究、讨论、学习。2年多来群内学术气氛浓厚,解题高手辈出,群员数学资料共享。较为突出的是黑马和成都罗老师,他们坚守群的岗位,有问必答,有难必解,受到广大群员的尊敬和崇拜。在群员的建议下,我将群内讨论的数学问题和解题方法收集如下,以飨读者。
问题1
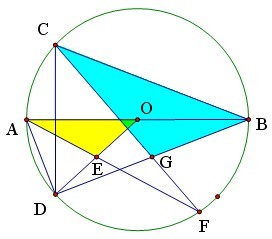
如图,AB是圆O的直径,弦CD⊥AB,E是OD中点,射线AE交圆于F,CF与DB交于G,求证:DG=GB。
证明:容易证明黄色三角形与蓝色三角形相似,因为AO:OE=2:1,所以CB:BG=2:1,即BG=DG。
问题2
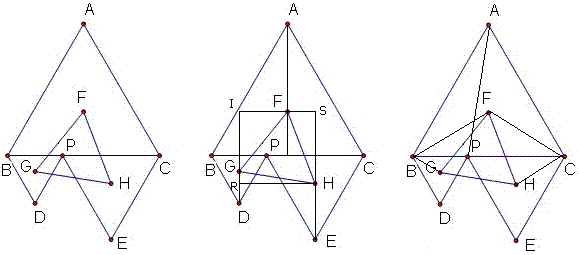
如图,有三个正三角形ABC,BDP,CEP,其中P在BC上,点F,G,H分别是这三个正三角形的重心,求证:△FGH为正三角形。
解法一:代数法
如图过F,G,H三点作矩形IRHS,设AB=2a,PB=2b,则可用a,b表示直角三角形IFG,SFH,HRG的三条斜边,而且表示的结果是一样的代数式。
方法二:几何法(高老师)
△BGF与△BPA相似,相似比为1比根号3;同样△CHF与△CPA相似,这样可以证明FG=FH; 然后利用刚才的相似,对应角相等,可以证明∠BFG+∠CFH=60度,即∠GFH=60度。
问题3
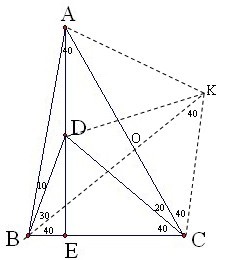
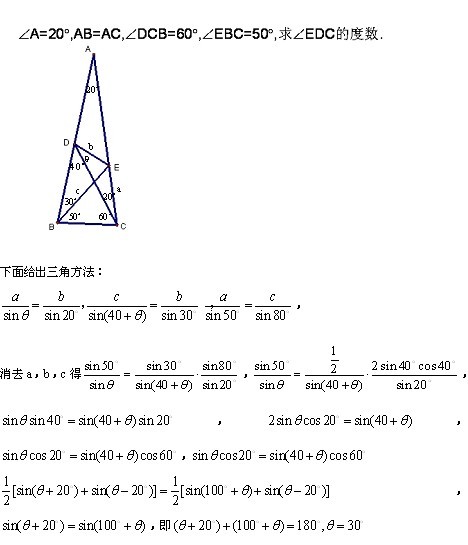
如图,点D在△ABC内,∠ABD=10°,∠ABC=80°,∠ACD=20°,∠BAC=40°,射线AD交BC于E。求∠AEC的度数。
解法一:
作∠DCB的平分线交AB于M,易知BC=CM=CD=AM,BM=DM,∠AMD=20度。
在CA上截取CG=MD,由∠DCG=∠AMD=20度,CD=AM,可证△AMD≌△DCG,
所以∠MAD=∠CDG, 且DA=DG,所以∠DAG=∠DGA,
设∠DAG=x,则由∠MAD=∠CDG得:40-x=x-20,解得:x=30,
于是∠AEC的度数=90度。
解法二:
以CD为边画等边三角形DKC,可以证明OA=OB,OK=OC,得BK=AC,
从而可以证明ΔADC≌ΔBDK,得AD=BD,即∠DAB=∠DBA=10°,
所以∠AEB=90° 。
问题4
已知如图,△ABC是等边三角形,D、E分别为AC、BC上的点,AE、BD交于F,且CD=BE,BD⊥CF,求AF与BF的比值。
黑马解:将△ABF绕B点顺时针旋转60°,至△CBM的位置,则容易证明CM:FM=1:2,即为所求。
问题5
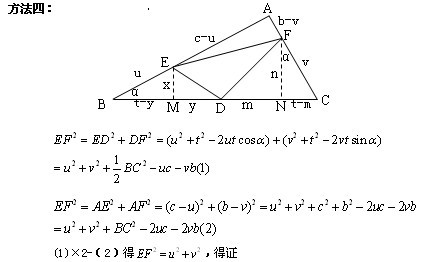
如图,在Rt△ABC中,∠A=90°,D为斜边BC的中点,E在AB上,F在AC上,∠EDF=90°,求证:EF^2=BE^2+CF^2.
解:将△BDE绕D点旋转180°至△CDG的位置,连结FGA,则可证GC=BE,FG=EF,∠FCG=90°,GF^2=CG^2+CF^2,即EF^2=BE^2+CF^2。
进一步思考:
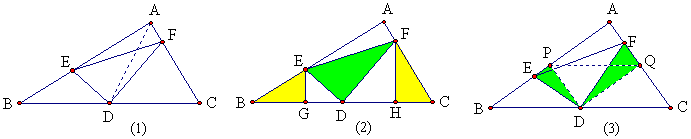
(1)王波明:如图1,可以用四点共圆的方法证明∠EFD=∠BAD=∠B,所以△DEF∽△ABC;
(2)成都罗老师:如图2,过E、F作BC的垂线EG,FH,则三块带颜色的三角形相似,且绿色三角形的面积等于黄色三角形的面积的和;
(3)成都罗老师:如图3,PQ为中位线,则两块绿色三角形相似;
(4)成都罗老师利用图2或图3证明本题的结论,其中图2中用到sin∠EDG+sin∠FDH=1.
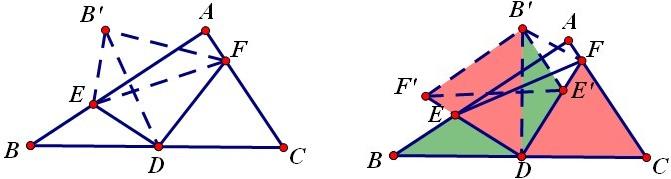
(5)黑马想到的方法很简单。
①作B点关于DE的对称点B’,则容易证明△B’DF≌CDF,且∠EB’F=∠EDF=90°.
②将△BDE绕D顺时针旋转90°,△DFC绕D逆时针旋转90°,容易证明△E’DF’≌EDF,所以E’F’=EF.
黑马的第4种方法:
问题6
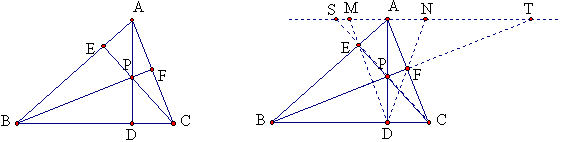
如图AD是△ABC的高,P是AD上任意一点,BP、CP延长后分别交对边于F、E,求证:∠ADE=∠ADF。
解:如图延长BF,DE,DF,CE,分别与过A点BC的平行线交于M,N,S,T,
由相似三角形得:\frac{AT}{BD}=\frac{AS}{CD}=\frac{AP}{PD}.
\frac{AT}{BC}=\frac{AN}{CD}=\frac{AF}{FC},\frac{AS}{BC}=\frac{AM}{BD}=\frac{AE}{EB}.
由以上关系不难得出:AM=AN,故AD是MN的中垂线,所以 ∠ADE=∠ADF。
问题7
已知a,b,c是有理数,求证:\sqrt{\frac{1}{(a-b)^2}+\frac{1}{(b-c)^2}+\frac{1}{(c-a)^2}}也是有理数。
叶士琴证明:设a-b=x,b-c=y,则c-a=-x-y,
则原式=\sqrt{\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{(x+y)^2}}=\sqrt{\frac{{x^2}{y^2}+(x^2+y^2)(x+y)^2}{{x^2}{y^2}(x+y)^2}}.
设xy=m,x+y=n,
则原式=\sqrt{\frac{m^2+(n^2-2m)n^2}{{m^2}{n^2}}}=\sqrt{\frac{n^4-2mn^2+m^2}{{m^2}{n^2}}}=\sqrt{\frac{(n^2-m)^2}{{m^2}{n^2}}}=\frac{n^2-m}{mn}.是有理数.
问题8
如图,直角梯形ABCD中,∠C=∠B=90°,AB=BC=4,以AD为边作正△ADE,E点正好落在BC上,求△CDE与△ABE的面积之比。
张良江解:如图补全一个正方形,设BE=x,则有4^2+x^2=2(4-x)^2,
解得x=8-4\sqrt{3},从而求出比值为2.
问题9
如图1,△ABC中,∠C=20°,AC=BC,M,N分别在AC,BC上,∠MBA=60°,∠NAB=50°,求∠NMB.
成都罗老师:方法1
如图2,作MK∥AB交BC于K,连结AK交BM于P,连结PN。
则△ABP和△MKP均为正三角形,
易证PB=AB=BN,故∠NPB=(180-20)÷2=80°,∠KPN=120-80=40=∠PKN,
所以NP=NK,所以△PMN≌△KMN,所以∠NMB=30°.
方法2:如图3
黑马的方法:
问题10
如图,已知正方形ABCD的面积为35平方厘米,EF分别AB,BC上的点,AF和CE相交于点G,并且△ABF的面积为5平方厘米,△BCE的面积为14平方厘米,求四边形BEGF的面积。
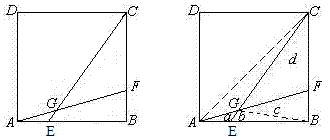
解:连结AC、BG,记S△AGE=a,S△EGB=b,S△BGF=c,S△FGC=d.
∵ BF:BC=S△ABF:S△ABC=2:7,同理 BE:BA=4:5,则有b=4a,d=\frac{5}{2}c.
由已知a+b+c=5,b+c+d=14,
即得四元一次方程组,可求得:b=\frac{28}{27},c=\frac{100}{27}.
因此:S_{BEGF}=b+c=\frac{128}{27}(平方厘米)
问题11
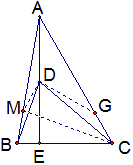
如图,P是等腰△ABC内一点,∠ABP=30°,∠CBP=40°,∠ACP=50°,∠BCP=20°,求证:(1)∠CAP=30°;(2)PA=PB+PC。
解:(1)作△ABP的轴对称△ACD,连结PD,延长CP交AB于F,作△APD的高AE.
易证BP=PD=DC,PE=ED,∠BFP=90°,PF=\frac{1}{2}PB=PE,
所以△APF≌△APE,所以∠PAF=∠PAE=∠DAE=∠DAC=10°,即∠CAP=30°;
(2)作△ABP的轴对称△ABG,连结PG,则△BPG是正三角形,C,P,G在一直线上,
所以PA=GA=GC=GP+PC=PB+PC.


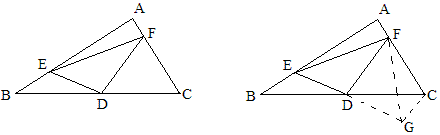
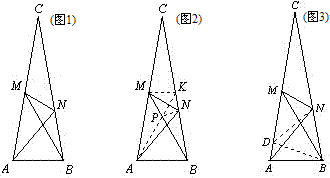

力挺
黄老师:整理得很好!为我们一些不能常在线的老师提供了很好的资料,希望以后看到更多!