新课引入是一节课成败的关键所在,我在以前写过《新课引入策略谈》,这儿想通过几个实例,具体地说明有些新课可以怎样引入。由于新课引入的方法各人有各自的方法,所以还望同行给出更好的方法,给予点评。
一、“有理数乘法”的教学
今天我们来计算下列运算:
3×2,(-4)×5,(-6)×(-7)
第一个是6,第二个可以理解成5个-4相加,对于第三个我们可以这样进行:
(-6)×(-7)=(-6)(1-8)=1×(-6)-8×(-6)=-6-(-48)=-6+48=42
这样得到3×2=6,(-4)×5=-25,(-6)×(-7)=42
请同学们得出两个有理数相乘的法则。
二、“平方根”概念教学
问题:
1、3的平方是多少?如何用算式表示计算的结果?这种运算叫做什么?
答:3的平方是9,用算式表示计算的结果是3^2,这种运算叫做平方(或乘方)运算。
2、什么的平方是9?如何用算式表示计算的结果?这种运算叫做什么?
答:±3的平方是9,用算式表示计算的结果还不会,运算名称还不知。
3、每次出现新的运算都得引进运算符号,如2个3相加记作“2×3”,2个3相乘记作“3^2”,那怎样表示平方得9的数呢?
由于这种运算的英文名称是“square root”,国外数学家就将字母 r 拉长,演变成\sqrt{\quad},这个符号就是“根号”,表示运算符号,所以平方得9 的数就表示为“±\sqrt{9}”,读作“正负根号9”,这种运算叫做“开平方”,它的结果叫做“平方根”.
4、几种运算概念比较
| 运算含义 | 符号 | 运算名称 | 结果名称 |
|---|---|---|---|
| 2个3相加 | 2×3 | 乘法 | 积 |
| 2个3相乘 | 3^2 | 平方 | 幂 |
| 平方得9的数 | ±\sqrt{9} | 开平方 | 平方根 |
5、加法和减法互为逆运算,乘法和除法互为逆运算,开平方和平方互为逆运算。
三、“三角形内角和”教学
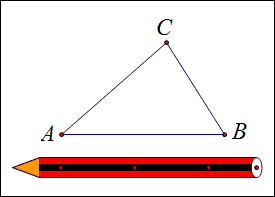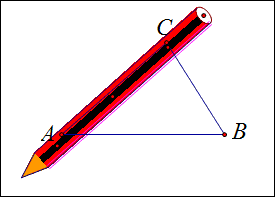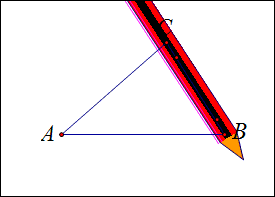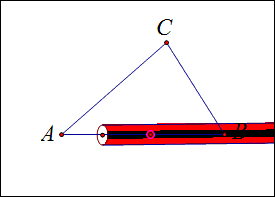
1、如图,展示一个三角形ABC;
2、利用一支铅笔,每次同一方向转过每个内角;
3、注意开始和结束时笔头方向相反,这就说明一共转了180°.
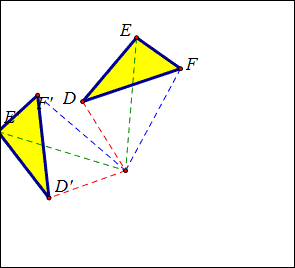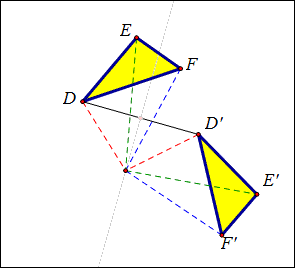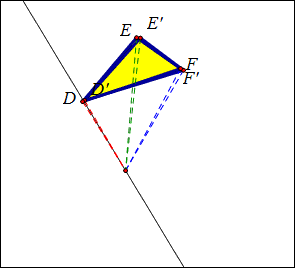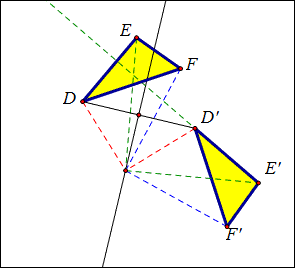
四、“旋转变换”教学
1、展示两个三角形,其中一个绕点O旋转,可以与另一个重合;
2、三角形所有顶点和旋转中心O连结,发现对应点和O的距离相等;
3、连结一对对应点D和D‘,再作DD’的中垂线,发现它必过O点;
4、延长E’D’,发现DE和E’D’所成的角等于旋转角,即对应线段所成的角等于旋转角。
五、“因式分解概念”教学
问题:
1、求2×3×5的多少,是乘法运算,将30写成2×3×5叫什么?
2、小学里的因数分解有哪些作用?
答:作用有:约分、简便运算、解决某些应用题。
3、2a(a-3b)是多少?把这个等式倒过来写,得到第二个等式,前者叫什么运算?后者运算名称怎么取?
4、乘法和因式分解能说成是互为逆运算吗?
5、猜想因式分解有哪些作用?
6、在因式分解的概念中,哪几个是关键词?
答:多项式、整式、积的形式
六、“直角三角形斜边上的中线等于斜边的一半”的教学
引入问题:
(1)如图,Rt△ABC中,∠C=90°,如何在AB上找一点D,使DA=DC?
(2)请证明:CD=BD。
(3)CD是△ABC的什么线?
(4)CD和AB有何关系?
(5)用语言叙述这个规律。
七、“勾股定理”的教学
问题:
(1)已知直角三角形ABC的直角边分别是3和4,求斜边AB。
如果学生有困难,可以提醒大家以前我们有将4个全等的直角三角形拼成正方形的做法。
(2)当直角边为5和12时,求斜边AB。
(3)当直角边为5和10时,求斜边AB。
(4)当直角边为a和b,斜边为c时,求a、b、c的关系。
(5)用语言叙述这个规律。
八、“一次函数”第二课时
本课时的教学主要是例3
某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长。据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区日沙漠面积的变化?
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区日沙漠面积将增加到多少公顷?
以及“待定系数法”。
首先例3中的问题(1)的表述学生不理解,什么叫做“描述”?
建议:
1、去掉问题(1),直接求问题(2),
2、老师什么都不要讲,直接让学生自己解题,用意是让用小学方法解题的学生遇到困难;
3、当多数学生不会解的时候,老师再讲“先求解析式,再解决问题”的方法;让学生体会到解应用题的方法不仅仅局限于算式、方程、代数式,函数也是常有的方法。
九、“一次函数的图象”第一课时
第一次画一次函数图象,老师一般都采用“描点法”,有一部分学生在以后的练习中居然忘了“两点法”。依然用“描点法”。为了避免这个现象,我采用以下的引入方法。
1、先讲函数图象的意义;
2、如图画一条过原点的直线,发现这条直线上所有点(x,y)都满足y=2x;
3、这说明这条直线就是函数y=2x的图象;
4、将这条直线向上平移1个单位,发现这条直线上所有点(x,y)都满足y=2x+1;
5、这说明这条直线就是函数y=2x+1的图象;
6、于是我们发现任何一次函数的图象都是一条直线;
7、既然是直线,我们可以用两点来确定这条直线。
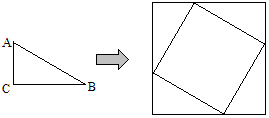
十、“矩形”第一课时
做一个平行四边形活动框(最好用几何画板),提问如下:
1、拉动平行四边形框,平行四边形的什么变化?什么不变?
2、变化的面积何时有最大值?这时平行四边形成为什么图形?
要说明为什么当∠A=90°时,面积最大。
3、连结两条对角线,发现对角线有什么现象?
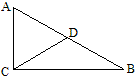
十一、三角形中位线性质
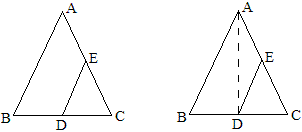
1、先讲三角形中位线的定义;
2、然后在等腰三角形中探索三角形中位线的性质
如图△ABC中,AB=AC,D、E分别是BC、AC的中点,请猜想DE和AB的数量关系和位置关系,并加以证明。
猜想:DE=\frac{1}{2}AB且DE∥AB。证明时连结AD,利用三线合一、斜边上中线性质。
3、当三角形是一般三角形时上述结论依然成立吗?学生会说成立,但难以证明。
老师启发如下:
原来由于等腰三角形,所以中线AD就是高,现在AD只是中线了。我们就会想到中线有什么性质?对!中线平分三角形的面积。
这样就有S_{\triangle{EDC}}=S_{\triangle{EDA}}=\frac{1}{2}S_{\triangle{ABD}},
可是解决问题仍有困难,我们试着再连结BE,如下图。
由面积方法得出S_{\triangle{ABE}}=S_{\triangle{ABD}}=\frac{1}{2}S_{\triangle{ABC}},所以△ABE和△ABD同底等高,即DE∥AB。
又因为S_{\triangle{ADE}}=\frac{1}{2}S_{\triangle{ABD}},且△ADE和△ABD等高,所以底边DE是底边AB的一半,即DE=\frac{1}{2}AB。

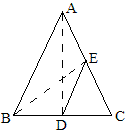
简洁明了,不像我们现在引入新课是不是拖拉要不什么都不是呵呵!受益匪浅!
向您学习!洗去浮尘方见金!实践如果没有思考就没有智慧!
认识黄老师是福分,受益匪浅。这些引入直白、精辟、有效。
黄老师的新课引入大开眼界,尤其是勾股定理真是出奇不意,斜边上中线等于斜边一半也很妙,妙不可言。精巧迅速,远比那些哗哩胡哨的情景创设强千倍。建议黄老师出一本书“新课引入百例谈”必畅销。