福建省莆田市2008年初中毕业、升学数学试卷中有这样的一道题:
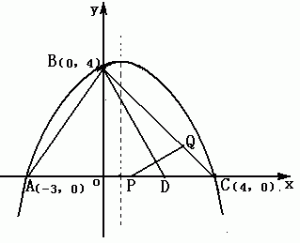
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1)求抛物线的解析式.
(2)已知AD = AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值;(第3小题略)
参考答案里写出的第2小题的解法是:
连接DQ,在Rt△AOB中,AB=\sqrt{OA^2+OB^2}=\sqrt{3^2+4^2}=5
所以AD=AB= 5,AC=AO+CO=3 + 4 = 7,CD = AC -AD = 7 – 5 = 2,
∵BD垂直平分PQ,所以PD=QD,PQ⊥BD,∴∠PDB=∠QDB.
∵AD=AB,∴∠ABD=∠ADB,∠ABD=∠QDB,
∴DQ∥AB,∴∠CQD=∠CBA.∠CDQ=∠CAB,∴△CDQ∽△CAB,
∴\frac{DQ}{AB}=\frac{CD}{CA} 即 \frac{DQ}{5}=\frac{2}{7},DQ=\frac{10}{7}.
∴AP=AD – DP = AD – DQ=5 – \frac{10}{7}=\frac{25}{7},t=\frac{25}{7}\div1=\frac{25}{7}.
其实,我们还可以连结BP,由PQ被BD垂直平分,得∠1=∠2,又由AD=AB,得∠ADB=∠ABD,从而可以证得∠APB=∠ABC,于是△ABP∽△ACB,所以AB^2=AP\times{AC},解出t=AP=\frac{25}{7} .
这两种方法都运用了几何性质,即由AD=AB,得出∠ADB=∠ABD,从而证得三角形相似. 如果AD≠AB,这种方法就难以奏效.
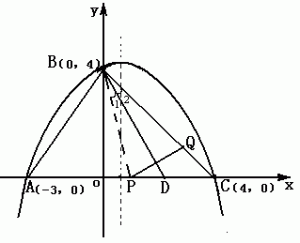
在浙江省宁波市某初中的一次初三数学月考中,借用了这道题,一位考生如下解答:
连结BP(如图),在Rt△AOB中,AB=\sqrt{OA^2+OB^2}=\sqrt{3^2+4^2}=5
∴AD=AB= 5,OD = AD -OA = 5–3 = 2,
∴ tan\angle{BDO}=\frac{4}{2}=2, ∴ \angle{BDO}=tan^{-1}2,
∵OB=OC,∴∠C=∠B=45°,∴∠2=tan^{-1}2 -45°,
∵PQ被BD垂直平分,∴∠1=∠2,
∴∠PBO=45°-2( tan^{-1}2-45°)=135°-2 tan^{-1}2,
∴OP=OB×tan∠PBO=4×tan(135°-2tan^{-1}2 ).
这个结果由计算器计算可得,OP=\frac{25}{7},所以t=AP=\frac{25}{7}.
多么奇妙的解法!可惜的是,这么好的解法被有些老师否定了,理由是借用计算器.
宁波市早就允许考生带计算器进考场,这样的理由实在没有说服力.我认为,利用计算器用三角函数解几何题是一种新思路,应用相当广泛. 我在平时的教学中,经常留意这种方法的应用,下面再举几例,说明借助计算器利用三角函数解决几何问题这种新思路应该受到关注.
例1 如图,已知正方形ABCD中,E、F分别在DC、BC上,DE=3EC,EF平分∠AEC,求证:CF=BF.
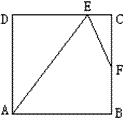
证明:∵tan∠AED=\frac{4}{3},∴∠AED=tan^{-1}\frac{4}{3},∠CEF=(180-tan^{-1}\frac{4}{3})\div2,
设CE=a,∴CB=4a,CF=CE•tan∠CEF=a(180-tan^{-1}\frac{4}{3})\div2=2a,
∴BF=2a, ∴CF=BF.
例2 如图,等腰直角三角形ABC中,∠C=90°,AE是三角形的角平分线,BD⊥AE交AE延长线于D,求证:AE=2BD.
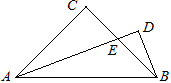
证明:∵∠CAE=22.5°,∴BD=ABsin22.5°,AB=\sqrt{2}AC,AC=AEcos22.5°,
∴BD=AEcos22.5°×\sqrt{2}×sin22.5°=0.5AE,即AE=2BD.
例3 如图,△ABC绕点B按逆时针方向旋转30°后得到△A´BC´,且BC=2,那么CC´的值是多少?(精确到0.01)
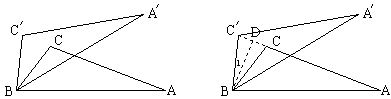
分析:以前,我们做这道题要借助于勾股定理,学生往往比较困难.
现在只要在图中作高BD,则∠1=15°,
所以CC´=2C´D=2BC´sin15°=2×2×\frac{\sqrt{6}-\sqrt{4}}{2}≈1.04.
你看,现在的计算器(CASIO fx-500ES或82ES)能显示sin15°的准确数\frac{\sqrt{6}-\sqrt{4}}{2},就算是去掉条件“精确到0.01”,也能求出答案来.
例4 如图,四边形ABCD是⊙O的内接正方形,P是弧AB的中点,PD交AB于E,则PE∶DE的值等于( )
A、\sqrt{2}-1 B、 \frac{\sqrt{2}-1}{2} C、 \frac{\sqrt{2}+1}{2} D、\frac{\sqrt{3}-1}{2}
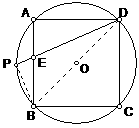
解:连结BD、PB. 设AD=1,则BD=\sqrt{2},PD=\sqrt{2}cos22.5°,DE=\frac{1}{cos22.5^\circ}.
接下来可以用计算器算出PE∶DE≈0.2071,再用计算器分别求A、B、C、D四个答案的近似值,发现\frac{\sqrt{2}-1}{2}≈0.2071,故选B.
在2008年各城市的中考试题中,发现有很多能运用计算器解决的题目,比如北京卷中的24题第3小题. 由此可见我们应该将计算器的使用嵌入到数学教学情景的整个计划中,不仅仅是代数问题,更应该关注几何问题.让学生的思维得到拓展,解题得以灵活,充分发挥计算器的功用,落实新课程的理念.
支持此解法。