反比例函数有许多性质,经过同行们的不断探索,又发现了新的性质,今列举如下,供大家研究。
1、如图,是两条反比例函数图象,它们是相似的。
相似的定义:若一条曲线经过缩放变换能与另一条曲线完全重合,那么这两条曲线称为相似的。
有关文章请参见《抛物线都相似》。
2、利用反比例函数图象可以画出两条已知线段的比例中项。
3、如图反比例函数图象与直线y=kx+m交于A、B两点,A点的坐标是(a,b).
(1)如图1,当m=0时,B点坐标是(-a,-b);
(2)如图2,当k=1时,B点坐标是(-b,-a);
(3)如图3,当k=-1时,B点坐标是(b,a).
这是反比例函数图象的对称性。
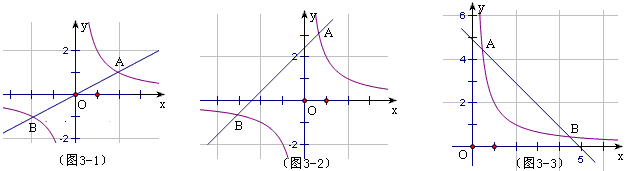
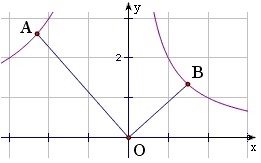
4、如图,A、B是反比例函数图象上任意两点,作AC⊥y轴于C,作BD⊥x轴于D,那么CD∥AB。
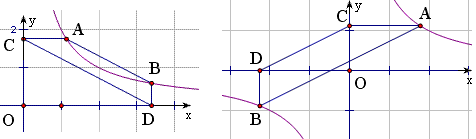
5、如图,A是x轴上任意一点,AB⊥x轴于A,交反比例函数图象于C,且BC=AC,BD⊥y轴于D,交反比例函数图象于E,那么DE=EB。
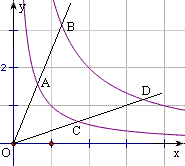
6、如图,射线OB交同一象限的两条反比例函数图象于A、B,且OA=AB,那么过O点的与这两条反比例函数图象相交于C、D的任意射线,均被截得相等的线段,即OC=CD。
7、如图,任一条直线与任意的反比例函数图象交于A、B,与坐标轴交于C、D,那么AC=BD。
8、如图,A在反比例函数y=-\dfrac{m}{x}图象上,B在反比例函数y=\dfrac{n}{x}图象上,且∠AOB=90°,那么OA:OB=\sqrt{m}:\sqrt{n}.
备注:连结AB,还可以用m、n表示sin∠A。
9、利用反比例函数图象可以证明不等式:
当n>0时,\dfrac{1}{n+1}+\dfrac{1}{n+3}>\dfrac{2}{n+2}。
解:如图设反比例函数为y=\frac{1}{x},A、E、B三点的横坐标分别为n+1,n+2,n+3,过这三点分别作x轴的垂线,交双曲线于D、F、C,直线DC和直线EF交于G,
则AD=\dfrac{1}{n+1},EF=\dfrac{1}{n+2},BC=\dfrac{1}{n+3},
由梯形中位线定理得:EG=\dfrac{1}{2}(\dfrac{1}{n+1}+\dfrac{1}{n+3}),
故\dfrac{1}{2}(\dfrac{1}{n+1}+\dfrac{1}{n+3})>\dfrac{1}{n+2},
即,\dfrac{1}{n+1}+\dfrac{1}{n+3}>\dfrac{2}{n+2}。
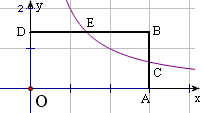
10、如图,双曲线y=\frac{k}{x}交OA的中点于D,AB⊥x轴于B,交双曲线于C,AC·OB=6,求k的值。
解:连OC,作DE⊥x轴于E,由已知△AOC的面积为3,
∵△ODE和△OCB的面积均为\dfrac{1}{2}k,由D是OA中点知:△OAB的面积=4△ODE的面积
∴\dfrac{1}{2}k+3=4\times\dfrac{1}{2}k,k=2.
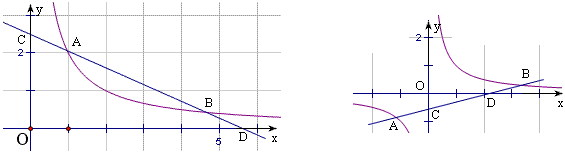
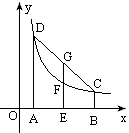
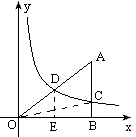
看过了,很好!
[latex]\frac{1}{n+1}+\sqrt{\frac{1}{n+1}}>x^2+y_1[/latex]