在全等三角形教学时,常常会碰到两个三角形满足两边及其中一边的对角对应相等的条件。而满足这样条件的两个三角形往往具备一些很重要的性质,如果不加以利用,就会使问题的解决发生一定困难。
我们知道,两个三角形如果满足两边及其中一边的对角对应相等是不能判定这两个三角形全等的。但不能错误地认为满足这样条件的两个三角形一定不全等。下面就以下六个方面谈谈我对这个问题的认识。
一、问题的引入
在进行全等三角形“边角边”公理教学时,我常喜欢问学生这么一个问题:
想一想,能否把边角边公理说成“有两边和一角对应相等的两个三角形全等”?(结合图形回答)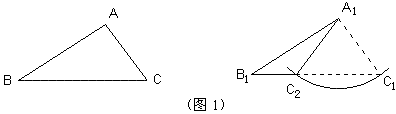
这是一个非常重要的数学知识,在这里包括了两个命题,其一就是SAS公理,它是真命题。其二就是“有两边和其中一边的对角对应相等的两个三角形全等”,这显然是一个假命题。例如在上面的图1中,AB=A1B1,∠B=∠B1,AC=A1C1,那么可以使△ABC≌△A1B1C1,也可以使这两个三角形不全等(如△ABC与△A1B1C2)。
二、定义
我们把两个三角形满足两边及其中一边的对角对应相等的现象叫做“SSA”。
三、SSA的教学的片段
等学生们学完了前面的内容之后,我问学生:
“同学们,前面我们每个同学都画了△ABC,使AB=8cm,BC=5cm,∠B=30°,结果每人得到的三角形都全等。现在我们将条件‘BC=5cm’改为‘AC=5cm’,使两边一夹角变为两边一对角,你再画出△ABC”。
话音刚落,大家就动手画了起来。片刻,大家基本上画好了,我布置了合作交流的任务:“请大家在四人小组里进行实验,用重叠法来判别一下你们所画的三角形是否全等”。
因为在巡视时我发现同学A所在的小组四人中,所画的三角形都彼此全等,所以请A先上来陈述。
A说:“我们四个人所画的三角形是全等的,这说明有两边和其中一边上的对角相等的两个三角形全等”。
我说:“同意A的人举手”。
哇!有一半以上的同学举手了。
我叫了没举手的B来陈述。
B说:“我们四人所画的三角形有两种,其中三人画的是图甲,只有我画的是图乙,我所画的三角形与他们不全等,这说明有两边和其中一边上的对角相等的两个三角形不全等”。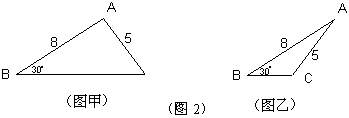
从同学们的眼光中我知道第一次举手的学生有一个共同的想法:我怎么没想到画图乙呢?
我说:“同意B的请举手”。
这时几乎全班同学都举手了。
我接着又问:“难道你们就没听出来B说话的破绽?哪个同学能完整的叙述一下?”
C说:“有两边和其中一边上的对角相等的两个三角形可能全等可能不全等”。
我说:“同意C的请举手”。
这时全班同学都举手了,我肯定了同学C所说的话是非常正确的。
接着我引导学生总结出“SSA”的两条性质。
四、SSA的基本性质
从上面的图1我们发现SSA有以下两条性质:
1.有两边和其中一边的对角对应相等的两个三角形可能全等,可能不全等。(所以不能利用“SSA”判定两个三角形全等)
2.有两边和其中一边的对角对应相等的两个三角形如果不全等,那么这两个三角形一定相差一个等腰三角形。
例1 已知△ABC和△A,B,C,中,使AB= A,B,=8cm,BC= B,C,=5cm,∠A=∠A,=30°, 如果△ABC和△A,B,C,不全等,求它们的面积之差是多少平方厘米。
解:本题没有图形,首先画出图3。由上面性质2可知,如果把这两个三角形重叠起来,就相差一个等腰三角形(如图3)。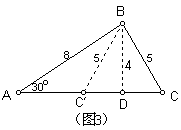
其中A与A,重合,B与B,重合,设C,落在BC上,作高BD,那么由几何性质知BD=4,CD=3,S△ABC=12,此即为问题的解。
五、SSA的三种类型
SSA在不同的情景、不同的问题中有三种基本类型:
1、 满足SSA的两个三角形可以全等可以不全等;
2、 满足SSA的两个三角形一定全等;
3、 满足SSA的两个三角形虽然不全等,但可以通过割去(或补上)一个等腰三角形来构造全等。
下面通过例子分别来说明这三种类型。
例2 如图4,AD=BC,∠CAB=∠DBA,问△ABC与△DBA是否一定全等?若一定全等请给出证明;若不一定全等请举出反例。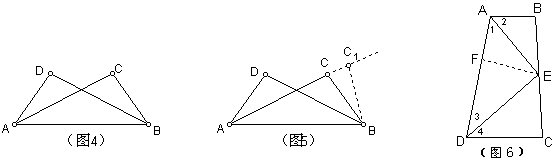
解:△ABC与△DBA满足的条件是AD=BC,∠CAB=∠DBA,AB=BA,是属于SSA,但它们不一定全等。
反例如图5,只要在直线AC上找到一点C1,使BC1=BC,那么△ABC和△ABC1总有一个与△DBA不全等。
此例属于SSA的第一类型。
例3 如图6,E是梯形ABCD的腰BC中点,AE平分∠BAD,在AD上取AF=AB,连EF,问△ABE是否与△AFE全等?△DFE是否与△DCE全等?
错解:由已知可得△ABE≌△AFE。而在△DFE与△DCE中,所满足的条件是FE=EC,∠AFE=∠C,DE=DE,属于SSA,所以无法判定△DFE是否与△DCE全等。
分析:其实以上第二对三角形虽然属于SSA,但却可以判定全等。方法是延长AE与DC交于G,即可利用等腰三角形“三线合一”定理来证∠3=∠4。
此例属于SSA的第二类型。
例4 如图7,四边形ABCD中,AC平分∠DAB,∠ABC+∠ADC=180°,求证:DC=BC。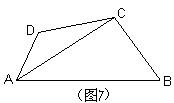
分析::在△ABC与△ADC中,满足的条件是∠BAC=∠DAC,AC=AC。另外,要求证的是DC=BC,这样三个结论就构成了SSA。现在这两个三角形之所以不全等是因为他们相差一个等腰三角形。
利用这个性质,可以用三种方法构造全等三角形。
方法一:在AD延长线上取一点E,使得CE=CD。(补上一个等腰三角形)
方法二:在AB上取一点E,使得CE=CB。(割去一个等腰三角形)
方法三:作CF⊥AB于F,CE⊥AD于E。(割去半个等腰三角形,同时又补上半个等腰三角形)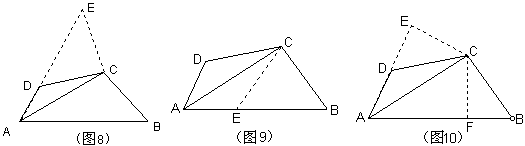
证明略。此例属于SSA的第三类型。
六、SSA的困惑
有时我自己也会被SSA问题难住,即无法判断是三种类型中的哪一种。
一天,一位学生拿着《同步练习》中的一道习题来问我:“黄老师,这道题是‘边边角’问题,我虽然知道不能判定三角形全等,但找不到不全等的反例。”
这道题是这样的:“如图11,在四边形ABCD中,AB=CD,∠B=∠D,问四边形ABCD一定是平行四边形吗?”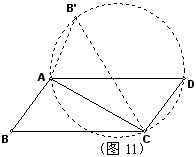
我想了许久,回答学生说:“一定!”
学生感到不解。
我自信地说:“我证明给你看,不过要用到你没学过的一条定理。”
证明:如图,将△ABC沿AC翻折得△AB′C,∵∠B=∠D, ∴∠B′=∠D,
∴A、C、D、B′四点共圆,∵AB=CD,∴AB′=CD,∴∠DAC=∠B′CA,
即∠DAC=∠ACB,∴△ABC≌△CDA,∴四边形ABCD是平行四边形。
待学生带着满脸疑惑走了之后,我静下心来思索,真的没有反例了吗?于是我就用几何画板做了一个课件。
如图,在几何画板中先任意画一个△ABC,然后以C为圆心、AB长为半径画圆,在圆C上任取一点D,再作射线DE,使∠EDC=∠ABC。我们可以让点D在圆C上移动而题设的条件不变,从而就会产生各种位置关系(如图12-1至12-4),其中使射线经过点A的位置就有两种。这说明满足条件的四边形有两个,反例找到了。所以这是一个假命题,上面的证明是错误的。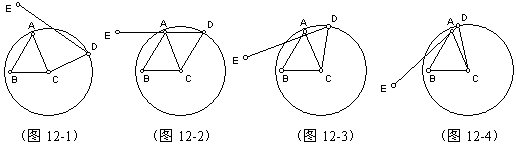
当我把这个事实告诉给这个同学的时候,他满意地笑了。
后记:这是我较早时候的文章,今天发表于此,供行家思考与点评。不过我想到了上面问题更好的反例了,如下图: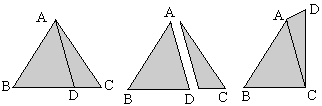
等腰三角形ABC中,AB=AC,D是底边BC上一点(非中点),沿AD将三角形剪开,再将△ADC翻折后与△ABD拼接,得到的四边形AB CD即为反例。