数学教学怎样培养学生的创新能力

10年前写的论文，被我随手一扔，今天整理资料时找到了它。读着自己失而复得的文章，虽然稚嫩了一点，可不舍得扔掉。于是花了一些时间打印于此，以作纪念。

目前的学生学习数学的现状是：依赖性强，希望继承小学的学习方法，套现成的公式、法则、模式，重结果轻过程，重怎么做轻怎么想，幻想获得一种万能的方法，或想通过题海战术提高解题能力。结果事与愿违，往往收获甚少，导致解题方法单一，缺乏专研精神和创新思维，碰到陌生问题便束手无策。我在教学过程中常用以下方法来拓展学生思维、培养创新能力。现介绍给大家，抛砖引玉，恳切希望得到同行指点。

一、讲授新课不拘泥于书本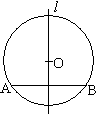

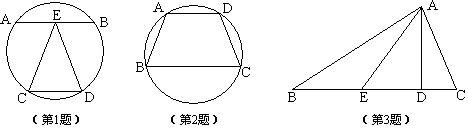
如垂径定理的学习中，可以启发学生发现如下命题：

如图，已知圆O和弦AB（不是直径），对于下列结论 ①直线 $l$ 过圆心O；②直线 $l$ 平分AB；③ $l$ ⊥AB；④ $l$ 平分劣弧 $\stackrel\frown{AB}$ ；⑤ $l$ 平分优弧 $\stackrel\frown{AB}$ 。已知其二便知其余。

切线性质定理有三个，也可以类似地缩成一个命题。

又如在学习正多边形的计算时，书本上给出了6个公式：

如图，AB是正n边形的一边，OB=r，那么①中心角∠AOB= $\frac{360^\circ}{n}$ ；②∠BOE= $\frac{180^\circ}{n}$ ；③边长AB= $2rsin\frac{180^\circ}{n}$ ；④周长c= $2nrsin\frac{180^\circ}{n}$ ；⑤边心距OE= $rcos\frac{180^\circ}{n}$ ；⑥面积s= $r^2sin\frac{180^\circ}{n}cos\frac{180^\circ}{n}$ 。

这么多的公式要学生记忆是困难的，也是没有必要的。我就干脆不讲这些公式，而是抓住正多边形的核心─等腰三角形或直角三角形，通过解直角三角形来解决所有正多边形的计算问题。

二、充分让学生畅所欲言

学生敢想敢言是培养创新能力的前提。一次在学习相似三角形的两个定理，即相似三角形的预备定理和比例线段判定平行后，我让学生填空：

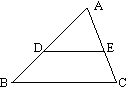如图，点D、E在△ABC的边AB、AC上， $\Rightarrow$ DE∥BC。

我鼓励学生方法越多越好，结果有角的条件，有比例的条件，其中一位叫史凤波的女生填上的条件是 $\frac{AD}{AB}=\frac{DE}{BC}$ 。

我不急于否定她的结论，叫大家判断这个推理是否符合定理条件，答：不符合。又问结论是否成立？学生回答：成立。问：为什么？学生无法回答。我就说：我们暂且把这个推理称为史凤波猜想，同学们回去后研究一下，你若认为正确的请给出证明，你若认为错误的请给出反例。

当学生无拘无束、敢想敢说时，他们便会暴露自己的想法，与教师交流。他们常指出我在教学中的漏洞，迫使我上课讲话十分严谨。

三、解题能力体现创新能力

目前学生有许多资料，常常附有解法。但我不满足于别人的解法，要求学生一题多解。一次做到一道题：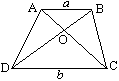

如图梯形ABCD的面积为s，AB∥CD，AB=a，CD=b（a<b），AC与BD交于O，若 $S_{\triangle{BOC}}=\frac{2}{9}s$ ，求a:b的值。

书上的解法是：

由 $S_{\triangle{AOD}}=S_{\triangle{BOC}}=\frac{2}{9}s$ ，设 $S_{\triangle{AOB}}=s_1$ ， $S_{\triangle{COD}}=s_2$ ，则 $s_1+s_2=\frac{5}{9}s$ .

又 $\frac{s_1}{S_{\triangle{BOC}}}=\frac{AO}{CO}=\frac{S_{\triangle{AOD}}}{s_2}$ ，∴ ${s_1}{s_2}=S_{\triangle{AOD}}\times{S_{\triangle{BOC}}}=\frac{4}{81}s^2$ ，

∴ $s_1,s_2$ 是方程 $t^2-\frac{5}{9}st+\frac{4}{81}s^2=0$ 的两个根，∴ $s_1=\frac{1}{9}s,s_2=\frac{4}{9}s$ ，

即 $\frac{s_1}{s_2}=(\frac{a}{b})^2=\frac{1}{4}$ ，∴ $\frac{a}{b}=\frac{1}{2}$ .

我为这种解法叫好，但不太容易想到，我就想到了另一种方法：

∵ $\frac{S_{\triangle{AOB}}}{S_{\triangle{DOC}}}=(\frac{a}{b})^2$ ，∴可以设 $S_{\triangle{AOB}}=a^2k,S_{\triangle{DOC}}=b^2k$ ，

∵ $\frac{S_{\triangle{AOB}}}{S_{\triangle{BOC}}}=\frac{AO}{CO}=\frac{a}{b}$ ，

∴ $S_{\triangle{AOB}}=abk=S_{\triangle{AOD}}$ ，

由已知 $abk=\frac{2}{9}(a^2+b^2+2ab)k$ ，∴ $a_1=2b,a_2=\frac{1}{2}b$ ，∴ $\frac{a}{b}=\frac{1}{2}$ .

我常常运用代数法、计算法、运动法、特殊值法、特征分析法、特殊图形法等等诸多方法，这些解题方法学生应用较少。通过反复训练，他们就会逐渐掌握这些方法，手里就会多了几种“武器”，使他们从僵化的思维中解脱出来。

四、自编数学题，拓展创新思维

学生缺乏哪一方面的解题能力，就应该找一些针对性的问题来训练，但有时这种题目不易找，还是自己动手编。比如我编过下列问题：

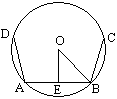
1、如图，E是弦AB（不是直径）中点，CD是弦（与AB不重合），EC=ED，求证：AB∥CD。

提示：此题考查学生灵活运用垂径定理的能力。设圆心为O，作CD的中垂线，则比过O点和E点，由垂径定理得OE⊥AB，∴AB∥CD。

2、如图，四边形ABCD是圆的内接等腰梯形，圆的半径是8，AB=CD=10，则梯形ABCD的面积的值是（）
A.是惟一的 B.有且只有二种 C.有且只有四种 D.无数种

提示：由于固定AB时，CD可以移动，所以选D。本题也可以问：当AB固定时，要使A、B、C、D四点构成等腰梯形，CD不能到达圆中的位置有处。（答案：4处）

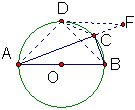
3、如图△ABC中AD是高，E在BC上，∠DAC=∠BAE，求证：△ABC的外心在直线AE上。

提示：作△ABC的外接圆，直线AE交圆于F，利用△ADC∽△ABF可得∠ABF=90°.

∴△ABC的外心在直线AE上。

4、在Rt△ABC中，∠C=90°，求sinA+sinB的最大值。

提示：如图，画△ABC的外接圆， $sinA+sinB=\frac{AC+BC}{AB}$ ，取上半圆的中点D，我们可以证明AC+BC≤AD+BD。

在AC延长线上取CF=CB，∵∠DCB=180°-∠DAB=135°，

∠DCF=180°-∠DCA=135°，∴∠DCB=∠DCF，∴△DBC≌△DFC，∴DF=DB，

∵AD+DF≤AF，∴AC+BC≤AD+BD。

于是 $sinA+sinB=\frac{AC+BC}{AB}$ ≤ $\frac{AD+BD}{AB}$ = $\sqrt{2}$ .

五、结合生活实例，促使知识迁移

生活中好的思维习惯可以促进数学能力的发展。反过来，数学中的思维能力可以改变生活习惯。

在讲授观察能力在数学中的重要性时，我问学生：你们有没有观察过，城市道路的路面上菱形标志的含义是什么？学生都说不知道。我就布置了这道观察生活的作业题。后来有个别学生作出了正确的判断。

一次，我要讲一道数学题：

当m为何实数时，方程 $x^2-(m-1)x-m-1=0$ 至少有一个非负根？

我先问学生：生活中我们遇到正面难以解决的问题，怎么办？比如大风总是把教室的门吹开，门锁又坏了，怎么办？学生缺乏经验，我就告诉学生的方法─关窗！正面难以解决时，考虑解决问题的反面。

回到这道题，考虑问题“至少有一个非负根”的反面“何时两根均为负数”，

即 $\left\{\begin{matrix}x_1+x_2<0\\ x_1x_2>0\end{matrix}\right.$ ， $\left\{\begin{matrix}m-1<0\\ -m-1>0 \end{matrix}\right.$ ，m<-1，

∴当m≥-1时，方程 $x^2-(m-1)x-m-1=0$ 至少有一个非负根。

六、写小论文，体验成功喜悦

我一直来主张学生写数学小论文，把课堂中学到的知识归纳出来，把别人想不到的东西写出来。每当我讲到有意思的数学问题，及时提醒学生，这便是小论文的题材。学生写过的小论文题目有：

浅谈综合法和分析法
配方法在代数式中的应用
整体思想之我见
运用因式定理巧妙分解因式
自编顺口溜，帮助记忆数学概念
不列竖式也能解决两个多项式相除
利用运动找对应关系
浅谈换元思想在因式分解中的应用
浅谈排除法
二元一次方程组的妙解

七、实践中学习数学

动手实践不但可以提高学生的动手能力，更容易培养创新思维，既可以在课堂内实践，也可以在课堂外实践。

如学习角平分线概念后，让学生用长方形纸片折出直角的平分线；学习圆柱、圆锥后，做一做它们的模型；学习中心对称后，让学生设计中心对称的商标；学习相似性及三角函数后，让学生用简易方法测量教学楼的高度；学习了三角形重心性质后，让学生用实验的方法验证三角形的重心是不是物理上的重心；过三角形的重心画一条直线是否一定把三角形的面积平分。