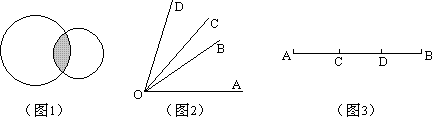重叠方法就是利用重叠原理的一种方法，在几何中两个（或多个）图形有重叠部分，重叠部分的面积就等于这两个（或多个）图形的面积减去总面积。重叠原理不仅可以求重叠部分的面积，还可以解决有重叠现象的线段、角及应用题等问题。
如下图，图1中重叠部分（阴影）的面积等于两圆面积和减去图形的总面积；图2中重叠部分的角∠BOC=∠AOC+∠DOB-∠AOD；图3中重叠部分的线段CD=AD+BC-AB。举例说明如下。
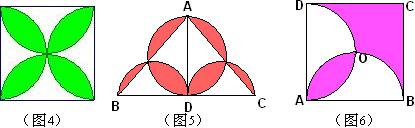
例1 如图4，正方形的边长为20，以边长为直径，画4个半圆，求绿色部分的面积（精确到0.1）
解：S绿色部分=4S半圆-S正方形=2л×102-202=200л-400≈228.3
这里将4个半圆进行重叠后，再减去图形的总面积正方形，就是重叠部分（绿色）的面积。
例2 如图5，等腰△ABC中，高AD=4cm，底边BC=6cm，以AD为直径画圆，分别以BD、CD为直径画半圆，求图中红色部分的面积。
分析：我们设想，先在桌子上放上图5中的一个圆纸片，再放上两个半圆纸片，这时有两块红色部分重叠了（即有两张纸），其余部分一张纸。我们再剪去一个三角形ABC，这样所有红色部分都有一张纸，其余没有纸片了。即
解：S红色部分=S圆+ S半圆+ S半圆-S△ABC=22л+1.52л-6×4÷2=6.25л-12.
例3 如图6，正方形ABCD的边长为8cm，分别以AB、AD为直径画半圆，求图中紫色两部分部分面积的差。
分析：我们设想，先在桌子上放上图6中的正方形ABCD，再剪去两个半圆纸片，这时紫色中的一个有一层纸，另一个（两个半圆的重叠部分）变成“-1”层了。所以有：
解：S大紫色部分– S小紫色部分=S正方形– S半圆– S半圆=82-42л=64-16л.
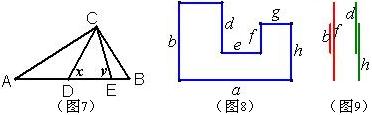
例4 如图7，△ABC中，∠ACB=90度，D、E在AB上，AE=AC，BD=BC，求∠DCE的度数。
解：设∠CDE=∠DCB=x度，∠CED=∠ECA=y度.
则∠DCE=x+y-90（这就是重叠原理，∠CED和∠ECA的重叠部分就是∠DCE）
因为x+y+(x+y-90)=180，∴x+y=135，∴∠DCE=45度
∵∴
例5 如图8是某零件的平面图，图中每个角都是直角，图中的8条线段分别用8个小写字母表示，为了测量这个图形的周长，只需测量图中8条线段中的哪几条？
解：我们将线段b、f和d、h移出来，放在图9的位置，可以清楚地看出总长一样、重叠部分也一样，所以b+f=d+h，又c+e+g=a, 所以只需测量a,b,f或a,d,h三段即可。
例6 在57个有理数中，正整数有3个，整数的个数比正数的个数的2倍少6个，负分数的个数比正数的个数的3倍少6个，求正数有几个。
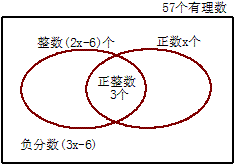解：如图，画出“文氏图”。设正数有x个（右圆圈中数的个数），那么整数有2x-6个（左圆圈中数的个数），负分数有(3x-6)个（圈外框内的数）。
∵两个圆圈数的总个数等于两个圆圈内数的个数和减去重叠部分正整数的个数，
∴整数和正数共有 [(2x-6)+x-3](个)，
由题意，得(2x-6)+x-3+(3x-6)=57，解得 x=12。答：正数有12个。
重叠方法，重叠原理还是重叠思想？怎么命名无关紧要，关键是归纳，把一些用同种方法解决问题的题串联起来，给学生点明这是同类题！我窃以为这种方法很有用，就惯于用这种方法教学，但效果没有我想象的好，为什么？我不清楚，我总是在反思自己，我的方法受到了挑战！还请同行指点，叩谢。