四、四边形中的基本模式
1、正方形
(1)正方形中的垂直线段
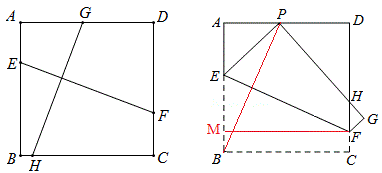
如图,在正方形ABCD中,EF⊥GH,那么EF=GH,反之亦然
例16 如图所示,现有一张边长为7的正方形纸片ABCD,点P为正方形AD边上的一点,AP=3,将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,求FG的长。
解:连BP,作FM⊥AB于M,由上模式,因为BP⊥EF,所以△ABP≌△MFE,所以ME=AP=3,
设GF=CF=MB=x,那么EP=EB=3+x,AE=4-x,由△AEP中的勾股定理得,(3+x)^2=(4-x)^2+3^2,
解得x=\frac{8}{7}。
注:连结PF利用两个直角三角形的公共斜边,解法更为简单。