大咖来了

2016年12月19日，宁波江北区在“北外”举行研究课和评课活动，应郑瑄邀请，罗增儒教授评课并作了讲座。

罗增儒教授简介

罗增儒，男，汉族，1945年1月生，广东省惠州市人，三级教授，课程与教学论（数学）博士研究生导师。1962年从惠州一中考入中山大学数学力学系数学专业，毕业后在陕西省耀县水泥厂当过矿山职工（10年）和子弟中学教师（8年），1985年底调入陕西师范大学数学系。曾先后担任陕西师范大学数学教育研究所所长、陕西师范大学教务处处长、陕西省数学会常务理事、陕西省中学数学教学研究会副理事长、西安市中学数学教学研究会理事长、《数学教育学报》编委、中国教育学会中学数学专业委员会学术委员、系中国数学奥林匹克首批高级教练。1994年10月起享受国务院政府特殊津贴，1999年获曾宪梓教育基金会全国高师优秀教师奖，2011年入选“国培计划”首批国培专家。

 

罗增儒教授坚持教学、科研平行发展，已为本科生开设了7门课程；为研究生讲授了3门课程。培养出硕士毕业生53人、博士毕业生6人。已在《教育研究》、《数学教育学报》、《数学通报》、《中学数学教学参考》等30多种刊物上发表文章400余篇，被《中国人民大学复印报刊资料》全文复印60余次（1983-2016）。在多家出版社出版了《数学竞赛教程》（陕西师范大学出版社,1993年）、《怎样解答高考数学题》（陕西师范大学出版社，1994年）、《怎样解答中考数学题》（陕西师范大学出版社，1996年）、《数学解题学引论》（陕西师范大学出版社,1997年）、《数学的领悟》（河南科学技术出版社，1997年）、《直觉探索方法》（大象出版社，1999年）、《中学数学课例分析》（陕西师范大学出版社,2001年）、《数学教学论》（陕西师范大学出版社，2003年）、《零距离数学交流》（广西教育出版社，2003年）、《数学教育概论》（高等教育出版社，2004年，参编）、《竞赛数学教程》（高等教育出版社，2005年，参编）、《中学数学解题的理论与实践》（广西教育出版社，2008年）、《高中数学解题阐宗》（黄河出版社，2010年）、《中学数学竞赛的内容与方法》（广西教育出版社，2012年）等书10多本。曾多次参与中学数学竞赛和数学高考的命题工作，已为初中联赛、高中联赛和冬令营提供了21道正式试题。主要工作有3个方向：

（1）数学教学艺术的理论与实践——形成“示范教学法”，实践“案例教学”。（2）数学解题论的基础建设——提出了“数学解题理论”。

（3）数学竞赛学的基础建设——搭起了“数学竞赛学”的一个理论框架。

罗增儒教授的工作曾获高校国家级优秀教学成果奖2次，省级优秀教学成果奖4次，省级优秀教材奖1次：

（1）示范教学法（1989年），高校省级优秀教学成果三等奖。

（2）奥林匹克数学学科建设（1993年），高校国家级优秀教学成果二等奖，省级一等奖。

（3）着眼数学素质服务基础教育——数学高考解题理论的建设（1995年），高校省级优秀教学成果二等奖。

（4）试办教育硕士学位的实践与探索（1999年），高校省级优秀教学成果二等奖。

（5）数学教学论课程建设与改革实践（2003年），高校省级优秀教学成果二等奖。

（6）21世纪高等师范院校学科教学论教材（2007年），陕西省高校优秀教材奖二等奖。

（7）构建西部教学团队、深化数学教育课程建设与教学改革、积极服务基础教育（2009年），高等教育国家级优秀教学成果一等奖。

这么高大上的人物以前只在照片中见过，今天终于见到真人了，好生激动。

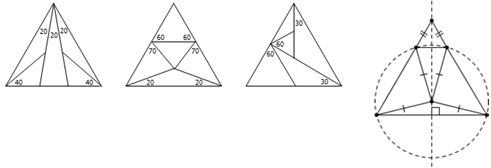
执教者方学士，执教课题是《三角形分割n个等腰三角形》，从特殊三角形到一般三角形，从n=2到n=3，再到n=4，直到n为任意的正整数。

罗教授将点评和讲座合二为一，对方老师的课很是赞赏，主要作了探究性学习和组合几何两个方面的介绍。

许多慕名前来的老师，济济一堂，600多人的音乐厅座无虚席，有来自于宁波各地的，有来自于嘉善的，有来自于……

罗教授说，探究性学习的基本过程有：

（1）创设情境；

（2）启发思考

（3）自主（或小组）探究

（4）协作交流

（5）总结提高

教授还指出探究性学习的优势和劣势。

主要优势是：

• 有利于发挥学生认识的积极性和主动性精神；
• 通过探索得来的知识记得牢、用的活，有利于知识的掌握与巩固；
• 有利于培养能力，发展智力．

主要局限：

• 费时、进度不好掌握，在课时比较紧张得时候只能够选择性应用．
• 比较适合小班教学，在大班级中实施有难度；
• 知识的系统性较难保证；
• 对中差生较难适应．

讲座中教授还提及研究性学习与讲授法的关系

讲授法以教师的系统讲解为主，教师进行适当的启发提问，引导学生进行积极思考， 使学生系统地掌握数学知识、基本技能，促进知识内化，形成新的认知结构．

主要优势：系统性强，经济高效，便于接受，是使用其它方法的基础

主要局限：教师主动、学生被动；利于知识掌握、无助能力培养；反馈功能弱；不利于因材施教；缺少体验．

教授总结道：

历史上是先有探究学习后有接受学习．讲授法不是万能的，没有讲授法是万万不能的．

在评课中教授提到了等边三角形5分割：

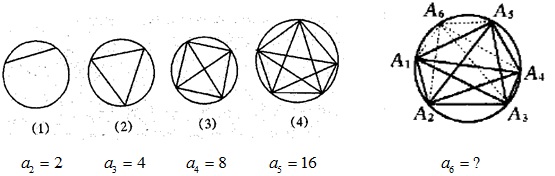
在讲组合几何时，教授展示了一道很有意思的题：

圆周上有n个点，两两连线无三线共点，将圆面分成了几块互不重叠的区域？

我们一一列举发现：设n个点时区域数为a_n，则当n=2时，a_2=2，当n=3时，a_3=4，当n=4时，a_4=8，当n=5时，a_5=16，于是有理由猜想a_n=2^{n-1}.

但却是错的。事实上

a_n=C_n^4+C_n^2+1=C_{n-1}^4+C_{n-1}^3+C_{n-1}^2+C_{n-1}^1+C_{n-1}^0

=\frac{1}{24}(n^4-6n^3+23n^2-18n+24).

这是一道说明猜想不能代替证明的好例子。

在与罗教授个别交流时，罗教授还说：探究性学习和研究性学习是不一样的，研究性学习是没有现成的方法可以参考，没有经验可以依托，是用数学研究实际生活里的问题，如方老师的课是探究性学习。

我问：我以前要求学生测量校园外的建筑物高度，不能出校园，工具不限，是不是研究性学习？

答曰：正是。

罗教授平易近人，谈吐风趣，只要问数学问题，总会给出权威的解答。他将自己水泥厂当矿工后从事数学教学比喻为：

好比是久别祖国的老华侨回到了故乡，好比是结束戎马生涯的老将军获得了第一次爱情。

足见老教授对数学的深爱。教授说初当老师期间，订阅了中国所有的数学杂志，每年订杂志的钱达到400多元，相当于几个月的工资，大多数的数学知识都是自学的，和华罗庚一样是自学成才的典范。而教授自喻是向全国老师学习的。

在去外滩途中，教授坐在副驾驶位，一定要系安全带，我说宁波这个位子不系也没关系，教授还是系上了，足见他的严谨和规范。

罗增儒教授曾说过：“解题好比是在黑屋子里摸东西，我们一会儿碰倒椅子，一会儿碰到桌子，好不容易摸到了目标物，然而解题远没有结束，此时我们应该拉开屋子里的电灯，看清楚屋子里的东西”。

餐桌上教授风趣地说：“一些人学数学是被领进门的，但门是什么样的都没看见。有一些门都没进，但却清楚看见了门内的所有东西，就是碰不着”。

我窃思，一定要追随教授的足迹，将数学进行到底。