平面几何中的几个著名定理

几何学起源于土地测量，几千年来，人们对几何学进行了深入的研究，现已发展成为一门具有严密的逻辑体系的数学分支，欧几里得的《几何原本》是其中最杰出的代表．人们从少量的公理出发，经过演绎推理得到不少结论，这些结论一般就称为定理．平面几何中有不少定理，除了教科书中所阐述的一些定理外，还有许多著名的定理，以这些定理为基础，可以推出不少几何事实，得到完美的结论，以至巧妙而简捷地解决不少问题．而这些定理的证明本身，给我们许多有价值的数学思想方法，对开阔眼界、活跃思维都颇为有益．有些定理的证明方法及其引伸出的结论体现了数学的美，使人们感到对这些定理的理解也可以看作是一种享受．尤其是在数学竞赛中应用广泛，作为经典世代相传。下面我们来介绍一些著名的定理．

1．梅涅劳斯定理

亚历山大里亚的梅内劳斯(Menelaus，约公元100年，他和斯巴达的Menelaus是两个人)曾著《球面论》，着重讨论球面三角形的几何性质．以他的名子命名的“梅内劳斯定理”，现载在初等几何和射影几何的书中，其逆定理是证明点共线的重要定理．

定理：

一直线与△ABC的三边AB、BC、CA或延长线分别相交于X、Y、Z，则\frac{AX}{XB}\times\frac{BY}{YC}\times\frac{CZ}{ZA}=1.

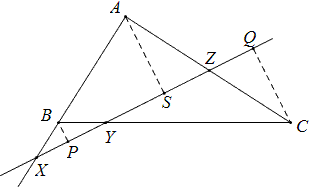
证明：

如图，过A、B、C分别作直线XYZ的垂线，垂足分别为S、P、Q．由△AXS∽△BXP得:\frac{AX}{XB}=\frac{AS}{BP}.

同理，\frac{BY}{YC}=\frac{BP}{CQ}，\frac{CZ}{ZA}=\frac{CQ}{AS}.

三式相乘得：\frac{AX}{XB}\times\frac{BY}{YC}\times\frac{CZ}{ZA}=1.

说明：

(1)如果直线与△ABC的边都不相交，而相交在延长线上，同样可证得上述结论，但一定要有交点，且交点不在顶点上，否则定理的结论中的分母出现零，分子也出现零，这时定理的结论应改为AX×BY×CZ=XB×YC×ZA，仍然成立．

(2)梅内劳斯定理的逆定理也成立，即“在△ABC的边AB和AC上分别取点X，Z，在BC的延长线上取点Y，如果\frac{AX}{XB}\times\frac{BY}{YC}\times\frac{CZ}{ZA}=1，那么X，Y，Z共线”．梅内劳斯定理的逆定理常被用来证明三点共线．

例1

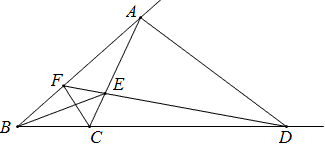
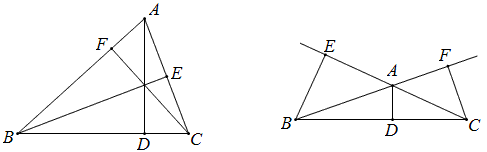
已知△ABC的内角∠B和∠C的平分线分别为BE和CF，∠A的外角平分线与BC的延长线相交于D，求证：D、E、F共线．

证明：

由角平分线性质定理得，\frac{AF}{FB}=\frac{AC}{BC}，\frac{BD}{CD}=\frac{AB}{AC}，\frac{CE}{EA}=\frac{BC}{AB}，

三式相乘得，\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1.

由梅内劳斯定理的逆定理知，D、E、F共线．

例2(笛沙格定理)

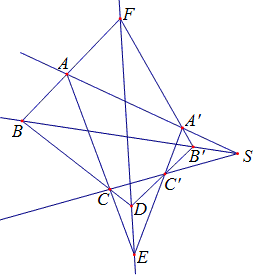
在△ABC和△A′B′C′中，若AA′、BB′、CC′相交于一点S，则AB与A′B′，BC与B′C′，AC与A′C′的交点F、D、E共线．

证明：

直线FA′B′截△SAB，由梅内劳斯定理得\frac{SA'}{A'A}\times\frac{AF}{FB}\times\frac{BB'}{B'S}=1，

同理，直线EC′A′和DC′B′分别截△SAC和△SBC，得

\frac{AA'}{A'S}\times\frac{SC'}{C'C}\times\frac{CE}{EA}=1，\frac{SB'}{B'B}\times\frac{BD}{DC}\times\frac{CC'}{C'S}=1，

将这三式相乘得，\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1，所以D，E，F共线．

2．塞瓦定理

意大利数学家塞瓦(G．Ceva)在1678年发表了下面的十分有用的定理，它是证明共点线的重要定理．

定理：

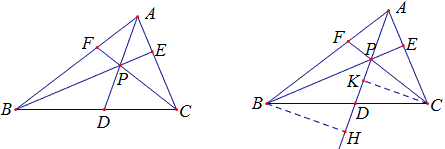
在△ABC内任取一点P，直线AP、BP、CP分别与边BC、CA、AB相交于D、E、F，则

\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1.

证明：

如图，过B，C分别作直线AP的垂线，设垂足为H和K，则

\dfrac{S_{\triangle{ABP}}}{S_{\triangle{ACP}}}=\dfrac{BH\times{AP}\div2}{CK\times{AP}\div2}=\dfrac{BH}{CK}=\dfrac{BD}{CD}.

同理，\dfrac{S_{\triangle{BCP}}}{S_{\triangle{ABP}}}=\dfrac{CE}{EA}，\dfrac{S_{\triangle{ACP}}}{S_{\triangle{BCP}}}=\dfrac{AF}{FB}.

∴\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1.

说明：

(1)如果P点在△ABC外，同样可证得上述结论，但P点不能在直线AB、BC、CA上，否则，定理的结论中的分母出现零，分子也出现零，这时，定理的结论应改为

BD×CE×AF=DC×EA×FB，仍然成立．

(2)塞瓦定理的逆定理也成立，即“在△ABC的边BC，CA、AB上分别取点D、E、F，如果\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1，那么直线AD、BE、CF相交于同一点．”

塞瓦定理的逆定理的证明，可以用“同一法”，即设BE、CF交于P，直线AD交BC于D’，由塞瓦定理证得D和D’重合。

塞瓦定理的逆定理常被用来证明三线共点．

例3

求证：三角形的三条中线、三条内角平分线和三条高所在的直线分别相交于同一点．

证明：

(1)如果D、E、F分别是△ABC的边BC、CA、AB的中点，则

\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=1.

由塞瓦定理的逆定理得中线AD、BE、CF共点．

(2)如果△ABC的内角平分线是AD、BE、CF，则

\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=\frac{AC}{CB}\times\frac{AB}{AC}\times\frac{AC}{AB}=1.

由塞瓦定理的逆定理得角平分线AD、BE、CF共点．

(3)设D，E，F分别是△ABC的高AD，BE，CF的垂足．

(i)当△ABC是锐角三角形时(如图3－103)，D，E，F分别在BC，CA，AB上，有BD=ccosB，DC=bcosC，CE=acosc，EA=ccosA，AF=bcosA，FB=acosB，

∴\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=\frac{bcosA}{acosB}\times\frac{ccosB}{bcosC}\times\frac{acosc}{ccosA}=1.

(ii)当△ABC是钝角三角形时，不妨设∠BAC是钝角，则有BD=ccosB，DC=bcosC，CE=acosC，

EA=ccos(180°-A)=-ccosA，AF=bcos(180°-A)=-bcosA,FB=acosB，

∴\frac{AF}{FB}\times\frac{BD}{DC}\times\frac{CE}{EA}=\frac{-bcosA}{acosB}\times\frac{ccosB}{bcosC}\times\frac{acosc}{-ccosA}=1.

(iii)当△ABC是直角三角形时，高AD，BE，CF都经过直角顶点，所以它们共点．

例4

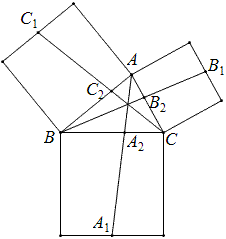
在三角形ABC的边上向外作正方形，A₁、B₁、C₁是正方形的边BC，CA，AB的对边的中点，证明：直线AA₁、BB₁、CC₁相交于一点．

证明：

如图，设直线AA₁、BB₁、CC₁与边BC、CA、AB的交点分别为A₂、B₂、C₂，那么BA₂:A₂C等于从点B和C到边AA₁的垂线的长度之比，即

\dfrac{BA_2}{A_2C}=\dfrac{S_{\triangle{ABA_1}}}{S_{\triangle{ACA_1}}}=\dfrac{AB\times{BA_1}\times{sin\angle{ABA_1}}\div2}{AC\times{CA_1}\times{sin\angle{ACA_1}}\div2}=\dfrac{AB}{AC}\times\dfrac{sin(\angle{B}+\angle{\theta})}{sin(\angle{C}+\angle{\theta})}.

其中∠θ=∠CBA₁=∠BCA₁．同理

\dfrac{CB_2}{B_2A}=\dfrac{BC}{AB}\times\dfrac{sin(\angle{C}+\angle{\theta})}{sin(\angle{A}+\angle{\theta})}，

\dfrac{AC_2}{C_2B}=\dfrac{AC}{BC}\times\dfrac{sin(\angle{A}+\angle{\theta})}{sin(\angle{B}+\angle{\theta})}.

将上述三式相乘得\dfrac{BA_2}{A_2C}\times\dfrac{CB_2}{B_2A}\times\dfrac{AC_2}{C_2B}=1.

根据塞瓦定理的逆定理，得AA₁、BB₁、CC₁共点．

3．托勒密定理

托勒密(Ptolemy，约公元85～165年)是古代天文学的集大成者．一般几何教科书中的“托勒密定理”(圆内接四边形的对边积之和等于对角线之积)，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．

定理:

如果四边形内接于圆，那么它的两对对边的乘积之和等于它的对角线的乘积．

证明：

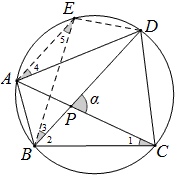
设四边形ABCD有外接圆O，AC和BD相交于P，∠CPD=α(如图)．若四边形ABCD的四边都相等，则四边形ABCD为圆内接菱形，即正方形，结论显然成立．若四边不全相等，不失一般性，设AB<AD，在\stackrel\frown{AD}上取一点E，使DE=AB，连结AE、BE、DE，则AE∥BD，于是△ABD≌△EDB，从而AD=BE．

由三角形面积公式S_△=\frac{1}{2}absinθ，可得四边形面积关系：

S_{四边形ABCD}=\frac{1}{2}AC×BD×sinα，

S_{四边形BCDE}=\frac{1}{2}(BE×BC+DE×CD)sin∠EBC，

又∵S_{四边形ABCD}=S_{四边形BCDE，}

∴(AD×BC+AB×CD)sin∠EBC=AC×BD×sinα．

由于∠α=∠DAC+∠ADB=∠DBC+∠EBD=∠EBC，

所以AD×BC+AB×CD=AC×BD．

说明：

(1)托勒密定理可以作如下推广：“在凸四边形ABCD中，AB×CD+AD×BC≥AC×BD．

当且仅当四边形ABCD是圆内接四边形时，等号成立．”

由此可知，托勒密定理的逆定理也成立．

(2)托勒密定理的证明方法很多，这里采用的是面积证法．还可采用相似三角形或余弦定理证明，请读者自行完成．

例5

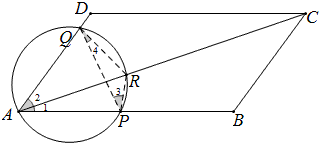
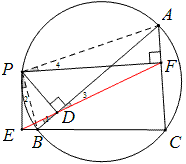
如图，过A的圆截平行四边形ABCD的边和对角线分别于P、Q、R，

求证：AP×AB+AQ×AD=AR×AC．

证明：

连结PQ，PR，QR．在圆内接四边形APRQ中，由托勒密定理得

AP×QR+AQ×PR=AR×PQ．

又因为∠1=∠2，∠3=∠4，所以△PQR∽△CAB，于是

\frac{QR}{AB}=\frac{PR}{BC}=\frac{PQ}{CA}

设上面的比值为k，并考虑到BC=AD，有QR=k•AB，PR=k•AD，PQ=k•CA，

于是可推得AP×AB+AQ×AD=AR×AC．

例6

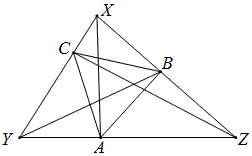
如图，等边△ABC内接于△XYZ，A在YZ上，B在ZX上，C在XY上，证明：

XA+YB+ZC<XY+YZ+ZX，并说明此中的“<”改为“=”是否可能成立。

证明：

对四边形ABXC运用托勒密定理，得AX•BC≤BX•AC+XC•AB，

所以AX≤BX+XC．

同样地BY≤CY+YA，CZ≤AZ+ZB．

将上述三式相加就得所要证明的不等式．

等号成立的充分必要条件是X，Y，Z在△ABC的外接圆上，但∠ZBX、∠XCY、∠YAZ都等于180°，因此等号成立只能是X、Y、Z分别与C、A、B重合的情况．

4、蝴蝶定理

蝴蝶定理(Butterfly theorem)出现过许多优美奇特的解法，其中最早的，应首推霍纳在职1815年所给出的证法。“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号，只因题目的图形象一只蝴蝶。这个定理的证法多得不胜枚举，至今仍然被数学热爱者研究，在考试中时有出现各种变形。至于初等数学的证法，在国外资料中，一般都认为是由一位中学教师斯特温首先提出的，它给予出的是面积证法，其中应用了面积公式：S=\frac{1}{2} bcsinA。1985年，在河南省《数学教师》创刊号上，杜锡录同志以《平面几何中的名题及其妙解》为题，载文向国内介绍蝴蝶定理，从此蝴蝶定理在神州大地到处传开。

定理：

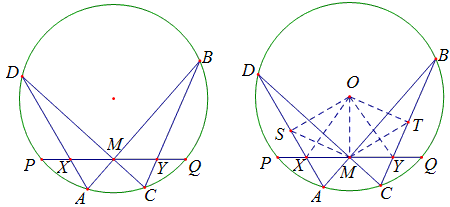
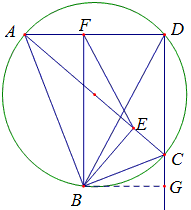
圆O中的弦PQ的中点M，过点M任作两弦AB，CD，弦AD与BC分别交PQ于X，Y，则M为XY之中点。

证明：

过圆心O作AD与BC的垂线，垂足为S、T，连接OX，OY，OM，SM，MT。

∵△AMD∽△CMB，∴\frac{AM}{CM}=\frac{AD}{BC}，

∵AS=\frac{1}{2}AD，BT=\frac{1}{2}BC，∴\frac{AM}{CM}=\frac{AS}{CT}，

又∵∠A=∠C，∴△AMS∽△CMT，∴∠MSX=∠MTY，

∵∠OMX=∠OSX=90°，∴∠OMX+∠OSX=180°，

∴O、S、X、M四点共圆，同理，O、T、Y、M四点共圆，

∴∠MTY=∠MOY，∠MSX=∠MOX，∴∠MOX=∠MOY ，

∵OM⊥PQ，∴XM=YM.

蝴蝶定理的应用例题正在搜索中……

5．西姆松定理

R. Simson. (1687-1768),英国数学家，曾于1756年校订欧几里得的《几何原本》。

定理：过三角形外接圆上异于顶点的任一点作三边的垂线，则三垂足共线。

已知： 若P是△ABC外接圆上任一点,自点P向△ABC的三边或延长线作垂线,垂足分别为D、E、F,

求证：D、E、F三点共线.

说明：过D,E,F的直线叫做△ABC关于P点的西姆松线。

证明：

连PA、PB，∵P、E、B、D及P、D、F、A四点共圆，

∴∠1=∠2，∠3=∠4，∵∠AFP=∠BEP，∠FAP=∠EBP，∴∠1=∠3，

∴D、E、F三点共线.

西姆松定理的逆定理：

若一点在三角形三边所在直线上的射影共线，则该点在此三角形的外接圆上。

证明：

如图，若D、E、F三点共线，连结BP，CP，

则因PE⊥BC，PF⊥AC，PD⊥AB，则有B、P、E、D和E、P、F、C分别四点共圆，

有∠PBD = ∠PED = ∠PCF.    故A、B、P、C四点共圆。

例7

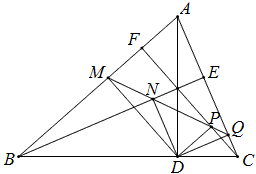
设△ABC的三条高为AD、BE、CF,过D作AB、BE、CF、AC的垂线,垂足分别为M、N、P、Q,求证：M、N、P、Q四点共线.

分析：要证四点共线,可先证三点共线.

略证：由∠AFC=∠ADC=90°，则A、F、D、C四点共圆，∴点D在△AFC的外接圆上.

又由M、P、Q是D点向△AFC的三条边AF、FC、CA所作垂线的垂足,

由西姆松定理知，M、P、Q三点共线，

同理可证：M、N、P三点共线，∴M、N、P、Q四点共线.

 例8

四边形ABCD是圆内接四边形，且∠D是直角，若从B作直线AC,AD的垂线，垂足分别为E,F，则直线EF平分线段BD.

证明：

作BG⊥DC于G，由西姆松定理G、E、F共线，

因为四边形BGDF是矩形，FG和BD互相平分，即直线EF平分线段BD.

6．斯台沃特定理

定理：

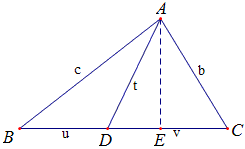
△ABC的边BC上任取一点D，若AB=c，AC=b，BD=u，DC=v，AD=t，则

t^2=\dfrac{b^2u+c^2v}{a}-uv.

证明：

过A作AE⊥BC，E为垂足(如图)，设DE=x，则有

AE²=b²-(v-x)²=c²-(u+x)²=t²-x²，

(若E在BC的延长线上，则v-x换成x-v．)

于是得\begin{cases} t^2=b^2-v^2+2vx\\ t^2=c^2-u^2-2ux \end{cases}

消去x得

(u+v)t²=b²u+c²v-uv(u+v)，即t^2=\dfrac{b^2u+c^2v}{a}-uv.

说明：

（1）当AD是中线时，u=v=\frac{1}{2}a，得三角形中线公式

t=\frac{1}{2}\sqrt{2b^2+2c^2-a^2}.

（2）当AD是△ABC的内角平分线时，由三角形的内角平分线的性质得

u=\dfrac{ac}{b+c}，v=\dfrac{ab}{b+c}，

∴t^2=\dfrac{b^2u+c^2v}{a}-uv=\dfrac{b^2ac+c^2ab}{a(b+c)}-\dfrac{a^2bc}{(b+c)^2}=bc-\dfrac{a^2bc}{(b+c)^2}

=\dfrac{bc[(b+c)^2-a^2]}{(b+c)^2}=\dfrac{bc(b+c+a)(b+c-a)}{(b+c)^2}，

设a+b+c=2p，得内角平分线长公式：

t_a=\dfrac{2}{b+c}\sqrt{bcp(p-a)}.

（3）当AD是高时，可得高线长公式

h_a=\dfrac{1}{2a}\sqrt{2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4}.

还可得三角形面积公式：S_{\triangle{ABC}}=\dfrac{1}{4}\sqrt{2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4}.

令a+b+c=2p，可得海伦公式：S_{\triangle{ABC}}=\sqrt{p(p-a)(p-b)(p-c)}.

例9

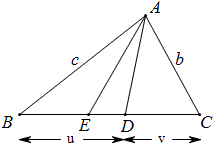
如图，在△ABC中，c＞b，AD是△ABC的角平分线，E在BC上，BE=CD．求证：
AE^2-AD^2=(c-b)^2．

证 为方便起见，设BD=u，DC=v，则BE=v，EC=u．由斯台沃特定理得

AD^2=\dfrac{b^2u+c^2v}{a}-uv，AE^2=\dfrac{b^2v+c^2u}{a}-uv.

因为AD是角平分线，所以\dfrac{u}{v}=\dfrac{c}{b}，

由合比定理得\dfrac{u-v}{u+v}=\dfrac{c-b}{c+b}.

∴AE^2-AD^2=\dfrac{b^2(u-v)-c^2(u-v)}{u+v}=\dfrac{(u-v)(b^2-c^2)}{u+v}=(c-b)^2

 

 

从网上搜到有61个几何著名定理（真的很吓人哦）：

1、勾股定理（毕达哥拉斯定理）

2、射影定理（欧几里得定理）

3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分

4、四边形两组对边中点的连线和两条对角线中点的连线交于一点（三线共点）

5、间隔地连接六边形的边的中心所作出的两个三角形的重心是重合的

6、三角形各边的垂直平分线交于一点

7、从三角形的各顶点向其对边所作的三条垂线交于一点

8、设三角形ABC的外心为O，垂心为H，从O向BC边引垂线，设垂足为L，则AH=2OL

9、三角形的外心，垂心，重心在同一条直线上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中点、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，

11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上

12、库立奇*大上定理：（圆内接四边形的九点圆）

圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

13、（内心）三角形的三条内角平分线交于一点，内切圆的半径公式：r=(s-a)(s-b)(s-c)s，其中s为三角形周长的一半

14、（旁心）三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点

15、中线定理：（巴布斯定理）设三角形ABC的边BC的中点为P，则有AB^2+AC^2=2(AP^2+BP^2)

16、斯图尔特定理：P将三角形ABC的边BC内分成m:n，则有nAB^2+mAC^2=(m+n)AP^2+mPC^2+nBP^2

17、波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，连接AB中点M和对角线交点E的直线垂直于CD

18、阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n（值不为1）的点P，位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上

19、托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC

20、以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形，

21、爱尔可斯定理1：若△ABC和三角形△都是正三角形，则由线段AD、BE、CF的重心构成的三角形也是正三角形。

22、爱尔可斯定理2：若△ABC、△DEF、△GHI都是正三角形，则由三角形△ADG、△BEH、△CFI的重心构成的三角形是正三角形。

23、梅涅劳斯定理：设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有

BP/PC×CQ/QA×AR/RB=1

24、梅涅劳斯定理的逆定理：（略）

25、梅涅劳斯定理的应用定理1：设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R，、∠B的平分线交边CA于Q，则P、Q、R三点共线。

26、梅涅劳斯定理的应用定理2：过任意△ABC的三个顶点A、B、C作它的外接圆的切线，分别和BC、CA、AB的延长线交于点P、Q、R，则P、Q、R三点共线

27、塞瓦定理：设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线，分别与边BC、CA、AB或它们的延长线交于点P、Q、R，则BPPC×CQQA×ARRB()=1.

28、塞瓦定理的应用定理：设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E，又设BE和CD交于S，则AS一定过边BC的中心M

29、塞瓦定理的逆定理：（略）

30、塞瓦定理的逆定理的应用定理1：三角形的三条中线交于一点

31、塞瓦定理的逆定理的应用定理2：设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T，则AR、BS、CT交于一点。

32、西摩松定理：从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线，设其垂足分别是D、E、R，则D、E、R共线，（这条直线叫西摩松线）

33、西摩松定理的逆定理：（略）

34、史坦纳定理：设△ABC的垂心为H，其外接圆的任意点P，这时关于△ABC的点P的西摩松线通过线段PH的中心。

35、史坦纳定理的应用定理：△ABC的外接圆上的一点P的关于边BC、CA、AB的对称点和△ABC的垂心H同在一条（与西摩松线平行的）直线上。这条直线被叫做点P关于△ABC的镜象线。

36、波朗杰、腾下定理：设△ABC的外接圆上的三点为P、Q、R，则P、Q、R关于△ABC交于一点的充要条件是：弧AP+弧BQ+弧CR=0(mod2∏).

37、波朗杰、腾下定理推论1：设P、Q、R为△ABC的外接圆上的三点，若P、Q、R关于△ABC的西摩松线交于一点，则A、B、C三点关于△PQR的的西摩松线交于与前相同的一点

38、波朗杰、腾下定理推论2：在推论1中，三条西摩松线的交点是A、B、C、P、Q、R六点任取三点所作的三角形的垂心和其余三点所作的三角形的垂心的连线段的中点。

39、波朗杰、腾下定理推论3：考查△ABC的外接圆上的一点P的关于△ABC的西摩松线，如设QR为垂直于这条西摩松线该外接圆珠笔的弦，则三点P、Q、R的关于△ABC的西摩松线交于一点

40、波朗杰、腾下定理推论4：从△ABC的顶点向边BC、CA、AB引垂线，设垂足分别是D、E、F，且设边BC、CA、AB的中点分别是L、M、N，则D、E、F、L、M、N六点在同一个圆上，这时L、M、N点关于关于△ABC的西摩松线交于一点。

41、关于西摩松线的定理1：△ABC的外接圆的两个端点P、Q关于该三角形的西摩松线互相垂直，其交点在九点圆上。

42、关于西摩松线的定理2（安宁定理）：在一个圆周上有4点，以其中任三点作三角形，再作其余一点的关于该三角形的西摩松线，这些西摩松线交于一点。

43、卡诺定理：通过△ABC的外接圆的一点P，引与△ABC的三边BC、CA、AB分别成同向的等角的直线PD、PE、PF，与三边的交点分别是D、E、F，则D、E、F三点共线。

44、奥倍尔定理：通过△ABC的三个顶点引互相平行的三条直线，设它们与△ABC的外接圆的交点分别是L、M、N，在△ABC的外接圆取一点P，则PL、PM、PN与△ABC的三边BC、CA、AB或其延长线的交点分别是D、E、F，则D、E、F三点共线

45、清宫定理：设P、Q为△ABC的外接圆的异于A、B、C的两点，P点的关于三边BC、CA、AB的对称点分别是U、V、W，这时，QU、QV、QW和边BC、CA、AB或其延长线的交点分别是D、E、F，则D、E、F三点共线

46、他拿定理：设P、Q为关于△ABC的外接圆的一对反点，点P的关于三边BC、CA、AB的对称点分别是U、V、W，这时，如果QU、QV、QW与边BC、CA、AB或其延长线的交点分别为ED、E、F，则D、E、F三点共线。（反点：P、Q分别为圆O的半径OC和其延长线的两点，如果OC2=OQ×OP 则称P、Q两点关于圆O互为反点）

47、朗古来定理：在同一圆同上有A1B1C1D14点，以其中任三点作三角形，在圆周取一点P，作P点的关于这4个三角形的西摩松线，再从P向这4条西摩松线引垂线，则四个垂足在同一条直线上。

48、从三角形各边的中点，向这条边所的顶点处的外接圆的切线引垂线，这些垂线交于该三角形的九点圆的圆心。

49、一个圆周上有n个点，从其中任意n-1个点的重心，向该圆周的在其余一点处的切线所引的垂线都交于一点。

50、康托尔定理1：一个圆周上有n个点，从其中任意n-2个点的重心向余下两点的连线所引的垂线共点。

51、康托尔定理2：一个圆周上有A、B、C、D四点及M、N两点，则M和N点关于四个三角形△BCD、△CDA、△DAB、△ABC中的每一个的两条西摩松的交点在同一直线上。这条直线叫做M、N两点关于四边形ABCD的康托尔线。

52、康托尔定理3：一个圆周上有A、B、C、D四点及M、N、L三点，则M、N两点的关于四边形ABCD的康托尔线、L、N两点的关于四边形ABCD的康托尔线、M、L两点的关于四边形ABCD的康托尔线交于一点。这个点叫做M、N、L三点关于四边形ABCD的康托尔点。

53、康托尔定理4：一个圆周上有A、B、C、D、E五点及M、N、L三点，则M、N、L三点关于四边形BCDE、CDEA、DEAB、EABC中的每一个康托尔点在一条直线上。这条直线叫做M、N、L三点关于五边形A、B、C、D、E的康托尔线。

54、费尔巴赫定理：三角形的九点圆与内切圆和旁切圆相切。

55、莫利定理：将三角形的三个内角三等分，靠近某边的两条三分角线相得到一个交点，则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。

56、牛顿定理1：四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点，三条共线。这条直线叫做这个四边形的牛顿线。

57、牛顿定理2：圆外切四边形的两条对角线的中点，及该圆的圆心，三点共线。

58、笛沙格定理1：平面上有两个三角形△ABC、△DEF，设它们的对应顶点（A和D、B和E、C和F）的连线交于一点，这时如果对应边或其延长线相交，则这三个交点共线。

59、笛沙格定理2：相异平面上有两个三角形△ABC、△DEF，设它们的对应顶点（A和D、B和E、C和F）的连线交于一点，这时如果对应边或其延长线相交，则这三个交点共线。

60、布利安松定理：连结外切于圆的六边形ABCDEF相对的顶点A和D、B和E、C和F，则这三线共点。

61、巴斯加定理：圆内接六边形ABCDEF相对的边AB和DE、BC和EF、CD和FA的（或延长线的）交点共线