初中数学里很多问题都涉及到平面图形的面积计算，所用到的方法繁多，而小学到底学了哪些方法呢？这个恐怕很多初中数学教师有所不知。结果就造成了“小学和初中都不教，而在初中却要考”的尴尬局面。所以“面积和面积法”是中小学数学衔接的真空地带。
于是初中数学教师一定要在合适的时候补上这一课，下面是我给学生补课的教案。
一、平移现象
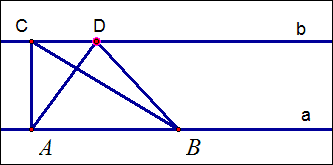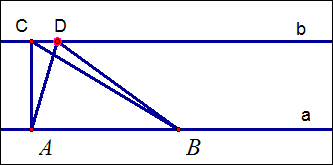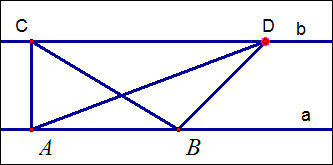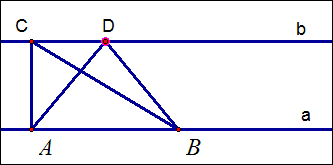
如图，直线a∥b，点A、B在a上，C、D在b上，则△ABC和△ABD的面积相等。即平移时面积不变。
依据：同底等高的两个三角形面积相等。
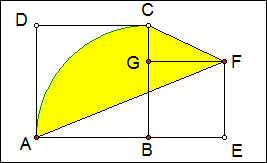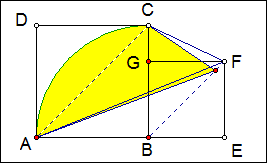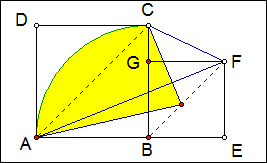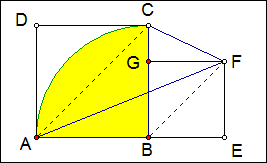
例1 如图，正方形ABCD的边长为6，正方形BEFG的边长为4，以B为圆心AB为半径画弧，连结CF、AF，求图中阴影部分的面积。
解：连结AC、BF，因为AC∥BF，所以S△ABC=S△ACF，即S阴影=S扇形BAC=9π.
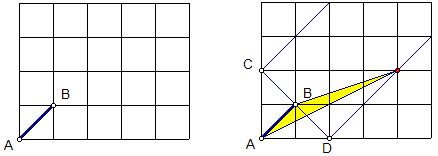
例2 如图，在正方形网格中，每个小正方形的边长为1，已有线段AB，在网格中找一格点，使得这一点和A、B两点组成的三角形面积为1，这样的点一共有 个。
如图，过点C、D且垂直于CD的直线上所有格点均符合条件，故符合条件的点共有7个。
例如图中的黄色部分面积就等于1，不用平移现象是很难想到的。
二、同高三角形
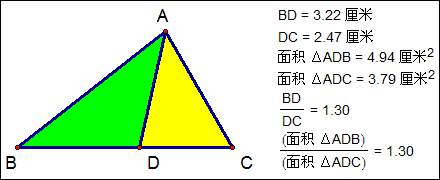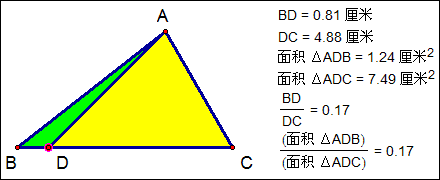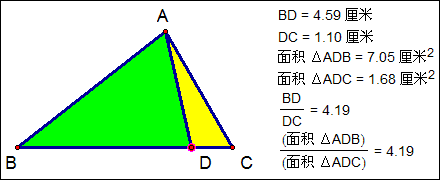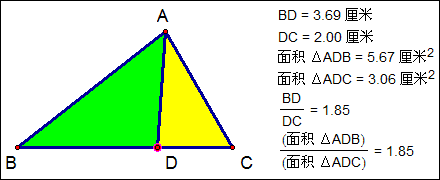
同高两个三角形的性质：如图D在△ABC的BC边上，则S△ABD:S△ADC=BD:DC。
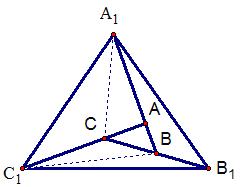
例3 如图延长△ABC的边CB、BA、AC分别至B1、A1、C1，使BB1=CB、AA1=3AB、CC1=2AC，若S△ABC=a，求S△A1B1C1。
解：连结A1C和C1B，∵△ABC与△A1AC是同高三角形，∴S△A1AC=3S△ABC=3a，
同理S△A1C1C=2S△A1AC=2×3a=6a，S△BC1C=S△B1C1B=2S△ABC=2a，
S△B1A1B=S△A1CB=a+3a=4a，∴S△A1B1C1=a+3a+6a+2a+2a+4a=18a.
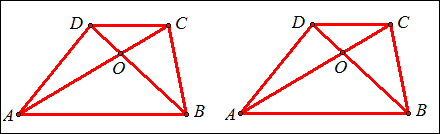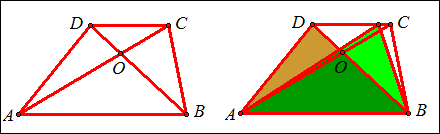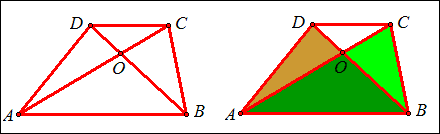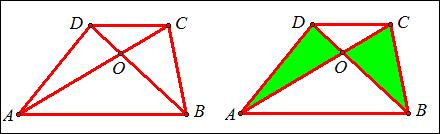
例4 如图，梯形ABCD中，AB平行CD，S△COD=4，S△BOC=6，S梯形ABCD。
解：∵AB平行CD，∴S△ABD=S△ABC，∴S△ABD-S△AOB=S△ABC-S△AOB，
即S△AOD=S△BOC=6，又∵△DOC和△BOC同高，∴DO:BO=4:6=2:3，
同理，△DOA和△AOB同高，∴S△AOD:S△AOB=∴DO:BO=2:3，
∴S△AOB=9，∴S梯形ABCD=4+9+6+6=25.
三、整体减部分
有些图形的面积要用稍大一点的图形面积减去几部分小的面积来实现，这种方法叫做“整体减部分”。
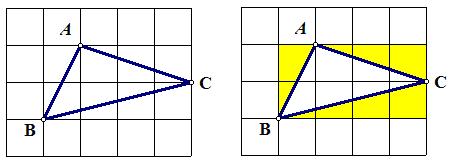
例5 如图，正方形网格每个小正方形的面积为1，求图中的三角形面积。
解：S△ABC=2×4-1-1.5-2=3.5 .
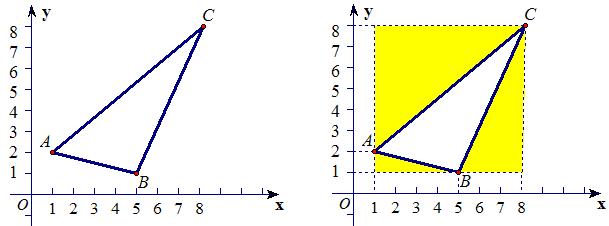
例6 如图，△ABC的顶点坐标分别是，A(1,2)，B(5,1)，C(8,8)，求S△ABC.
解：S△ABC=7×7-2-21-10.5=15.5 .
四、分割图形
有些图形的面积计算，要先进行分割。
例7 如图正三角形ABC中，D,E,F,G,H,I分别是各边的三等分点，S△ABC=18，求六边形DEFGHI的面积.
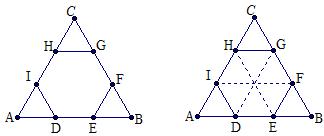解：不难证明这个六边形是正六边形，所以连结HE、DG、IF交于一点，故正三 角形被等分成6个小正三角形，S六边形DEFGHI=18÷9×6=12.
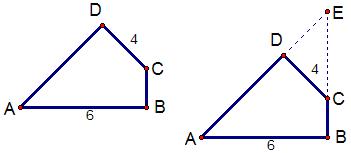
例8 如图四边形ABCD中，角A=90度，AD=6，AB=8，BC=24，CD=26，求四边形ABCD的面积。
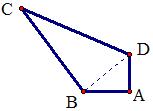解：连结BD，∵∠A=90度，AD=6，AB=8，∴BD=10，∵BC=24，CD=26， ∴∠CBD=90度，∴S四边形ABCD=6×8÷2+24×10÷2=144.
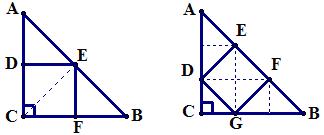
例9 如图，有两个全等的等腰直角三角形ABC，各画出了一个内接正方形CDEF和DEFG，请比较两个正方形的大小，并说明理由。
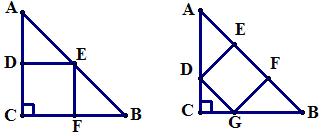解：如图将每个图形分割，则第一个正方形占总图形的1/2，第二个正方形占总图形的4/9，所以是第一个正方形面积大。
五、补上图形
某些图形求面积时，要先补上一块图形，再用整体减部分来计算。
例10 如图，四边形ABCD中，∠B=∠D=Rt∠，∠A=45°，AB=6，DC=4，求四边形ABCD的面积。
解：延长AD及BC交于E，由已知，△ABE、△CDE均是等腰直角三角形。
S四边形ABCD=S△ABE-S△CDE=\frac{1}{2}\times6^2-\frac{1}{2}\times4^2=10.
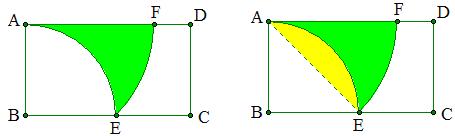
例11 如图，矩形ABCD中，AB=2，以B为圆心AB为半径画弧AE交BC于E，以A为圆心AE为半径画弧EF交AD于F，求绿色部分的面积.
解：连AE，则S绿色部分=S扇形-S黄色部分.
∵∠EAF=90°-45°=45°，
∴S绿色部分=\frac{45}{360}\pi(2\sqrt{2})^2-(\frac{90}{360}\pi\times2^2-\frac{1}{2}\times2^2)=2.
六、先割后补
这种方法就是先将图形进行分割，再将分割后的图形补到合适的位置，分为旋转割补、平移割补、反射割补和其它割补四种。四、五、六三种方法统称“割补法”。
例12 如图，四边形ABCD中，∠C=∠BAD=90°，AB=AD，四边形ABCD的面积为16，AE⊥BC于E，求AE的长。
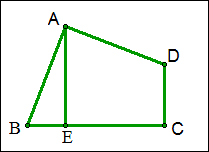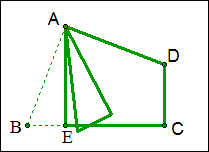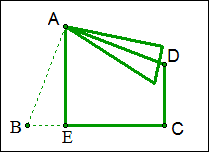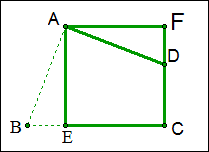解：将△ABE绕A点逆时针旋转90度至△ADF的位置，由已知可以证明四边形 AECF为正方形，而面积与四边形ABCD相等，故AE=\sqrt{16}=4.
例13 如图，正方形ABCD的边长为8cm，分别以AB、AD为直径画半圆，求图中紫色部分的面积.
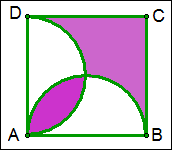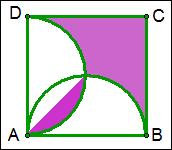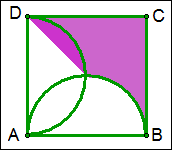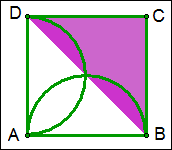解：S紫色部分=\frac{1}{2}\times8^2=32.
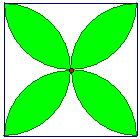
例14 如图，一个正方形的边长为a，以正方形的每个顶点为圆心，\frac{a}{2}为半径画4个圆，求图中花瓶（紫色部分）的面积.
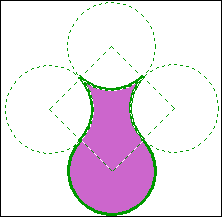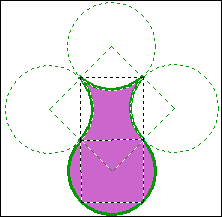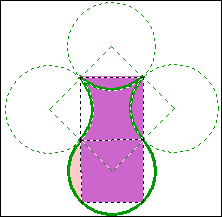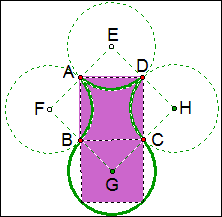解：S紫色部分=2S正方形ABCD=S正方形EFGH=a^2.
七、和差相等
同一个图形（或面积相等的两个图形）减去（或加上）面积相等的图形（或同一个图形）差（或和）相等。简单地说：
相等的面积加上相等的部分，和相等。相等的面积减去相等的部分，差相等。
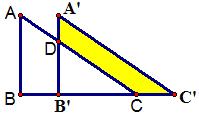
例15 如图，直角△ABC中，AB=5，将△ABC向右平移2，得到的像为△A’B’C’，B、B’、C、C’在同一直线上，A’B’与AC交于D，A’D=1，求黄色部分的面积。
解：∵S△ABC=S△DB’C+S四边形ABB’D，S△A’B’C’=S△DB’C+S四边形A’DCC’
∴S四边形A’DCC’=S四边形ABB’D=\frac{1}{2}(5+5-2)\times2=7.
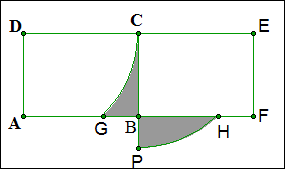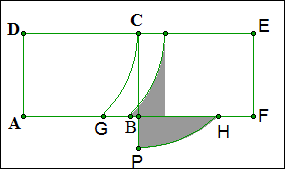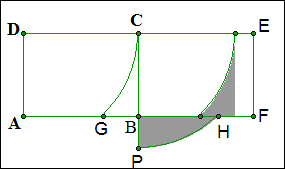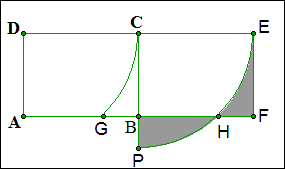
例16 如图两个完全相同的长方形ABCD和CDEF拼在一起，已知AB=1，AD=a，以A为圆心，a为半径画弧，交BC于G；以D为圆心，a 为半径画弧交DC延长线于P，交CF与H。（1）当两个阴影部分面积相等时，求a的值(π取3)；（2）当a=2时，求图中两个阴影部分面积之差的绝对值。
解:(1)将矩形ABCD内的阴影部分平移至矩形BCEF内，使G与H重合，
那么S扇形CPE=S矩形BCEF，即\frac{1}{4}\times3\times1^2=a，a=\frac{3}{4}.
(2)当a=2时，|阴影部分面积差|=|S扇形CPE-S矩形BCEF|=|\frac{1}{4}\times3\times1^2-2|=\frac{5}{4}.
八、重叠方法
就是利用重叠原理的一种方法，即两个（或多个）图形有重叠部分，重叠部分的面积就等于这两个（或多个）图形的面积和减去整个图形的总面积。
例17 如图，正方形的边长为20，以边长为直径，画4个半圆，求绿色部分的面积（精确到0.1）。
解：S绿色部分=4S半圆-S正方形=2π×102-202=200π-400≈228.3
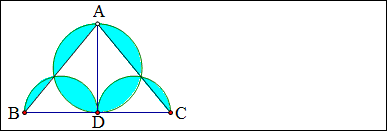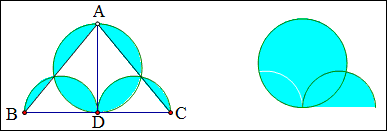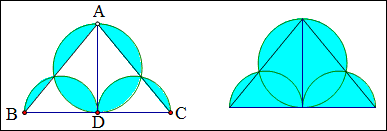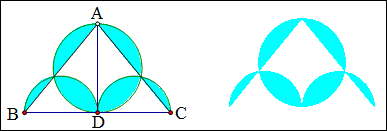
例18 如图，AD是△ABC的高，AD=6，BD=CD=4，以AD为直径画圆，以BD,CD为直径画半圆，求蓝色部分的面积。
解：我们设想桌面上先放一个圆形纸片，再放2个半圆形纸片，再揭掉一个三角形的纸片，这样原来2层纸的区域就成了一层纸，故
S蓝色=S圆+2S半圆-S三角形=3^2\pi+2^2\pi-\frac{1}{2}\times8\times6=13\pi-24.
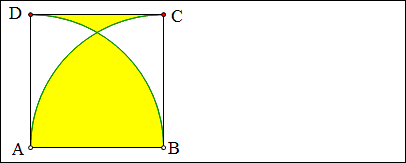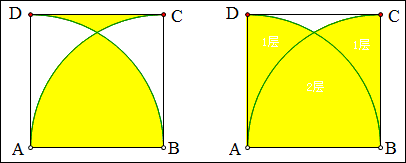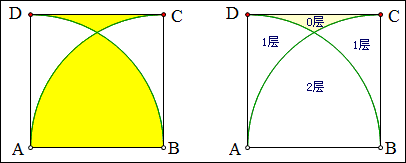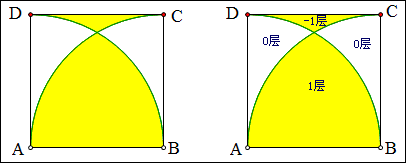
例19 如图，正方形ABCD的边长为2，以A,B为圆心，2为半径画2条弧，求图中黄色部分的面积差。
解：如图，我们设想桌面上先放一个直角扇形纸片，再放另一个直角扇形纸片，再揭掉一个正方形的纸片，这样原来2、1、0层纸的区域就成了1、0、-1层纸，故
S黄色部分差=2S直角扇形-S正方形=\frac{1}{2}\times2^2\pi-2^2=2\pi-4.
九、面积法
有些几何问题本身不涉及面积，通过面积的方法来解决显得特别简单。利用这种方法求垂线段的长度、证明垂线段相等尤为方便。
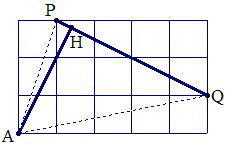
例20 如图在3×5的正方形网格中，每个小正方形的边长为1，求图中点A到PQ的距离AH的长。
解：连结AP,AQ则S△APQ=S矩形-S三个三角形=15-1.5-4-2.5=7,
∴\frac{1}{2}\times{AH}\times{PQ}=7,PQ=2\sqrt{5},∴AH=\frac{7}{5}\sqrt{5}.
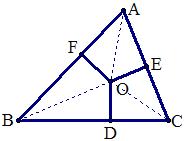
例21 如图△ABC中，S△ABC=4，AB+AC+BC=12,点O是△ABC内一点，且O到三边的距离相等，即OD=OE=OF,求OD的长。
解：连结OA,OB,OC,设OD=r，
则有S△ABC=S△OAB+S△OBC+S△OAC
=\frac{1}{2}\times{AB}\times{r}+\frac{1}{2}\times{BC}\times{r}+\frac{1}{2}\times{AC}\times{r}=\frac{r}{2}(AB+BC+AC).
即4=\frac{r}{2}\times12,r=\frac{2}{3}.
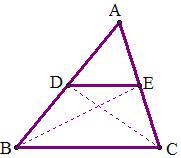
例22 用面积法证明三角形中位线定理.
已知：△ABC中，D,E分别是AB,AC的中点.求证：DE平行BC，DE=\frac{1}{2}BC.
解：连结BE,CD.由已知得S△BDE=S△ADE=S△CDE,
△BDE和△CDE同高，∴DE平行BC.
∵S△BDE=\frac{1}{4}S△ABC，S△BCD=\frac{1}{2}S△ABC,
∴S△BDE=\frac{1}{2}S△BCD,
∵△BDE和△CDE同高,∴DE=\frac{1}{2}BC.