今天是一节三角形中位线的复习课,课题是“变化多端的中位线”。
其中讲到四边形一组对边中点连线的问题:
如图,四边形ABCD中,E,F,分别是AD,BC的中点,
(1)如图(1),若AB=CD,G是BD的中点,求证:∠GEF=∠GFE。
(2)如图(2),求证:2EF<AB+CD。
第(1)题是为第(2)题服务的,是为第(2)埋下伏笔。
做完本题后,我说:第(2)题的解答方法我只想到一种,但我不敢说只有一种。
谁知下课时,课代表孙凌前来告知,她想到了第2种方法,她的方法是:
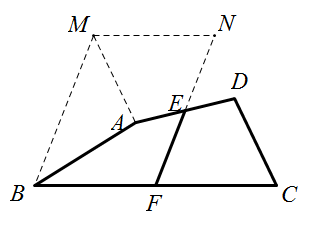 如图将四边形CDEF绕点E旋转180°至四边形MAEN,则得到平行四边形MBFN,
如图将四边形CDEF绕点E旋转180°至四边形MAEN,则得到平行四边形MBFN,
故2EF=FN=BM<AM+AB=AB+CD.
辛亏我讲话留有余地,多年来我真的只有一种方法解此题,孙凌的解法还印证了一个事实:条件中有中点,未必只有中位线一条路可走。
好样的孙凌,你是一个聪明的女孩,谁说巾帼不如须眉,你可以做到巾帼不让须眉。
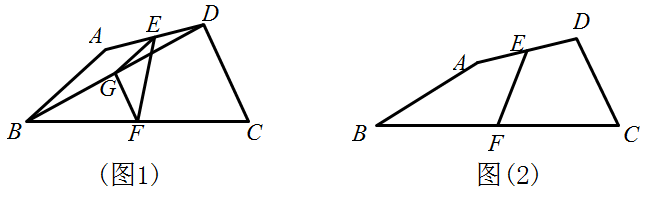
The discussion of connecting the midpoints of opposite sides of a quadrilateral is particularly interesting. I found a helpful visualization of similar concepts on https://seed3d.ai that might be useful for students.
timutainanlewobuhui
哇厉害666666不愧是课代表