教学内容:
三角形的角平分线、中线和高线。
教学目标:
1、通过折纸感受三角形主要线段概念的发生过程,经历由感性认识到理性认识的飞跃;
2、能辨认三角形的角平分线、中线和高线;
3、会画三角形的角平分线、中线和高线;
4、体会中线平分面积,角平分线所在的直线可以作为对称轴的基本思想;
5、了解三角形高的位置与三角形形状的关系;
6、能利用三角形主要线段所具有的数量关系解决问题。
重点与难点:
三角形主要线段的概念和相应的数量关系是本课的重点。
钝角三角形画高线很多学生容易出错,是本节课的难点之一,例2求角平分线和高线的夹角,数量关系较为复杂,是本课的难点之二。
教学过程
1、主要线段概念的发生过程
(1)因为在小学已经学习了高线的概念和画法,所以先来学习高线会显得比较自然。
小学阶段所学的高线概念比较感性的,如果通过折纸的方法折出高线,再给出高线的定义,课堂形式会比较生动。
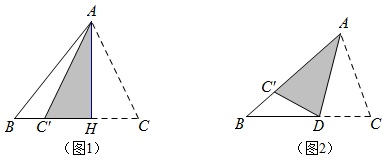
问题:任意剪一张三角形纸片,折出其中一条高线。
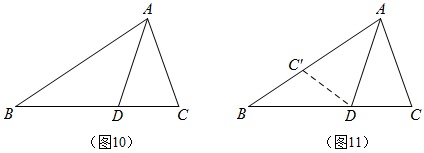
如图1,沿过点A的折痕折叠△ABC,使C落在BC上的C’,则折痕AH即为其中一条高线。
给出高线的定义,并问:一个三角形有几条高?
(2)三角形的角平分线是一个全新的概念,将上面折高线的方法稍微变化一下即得图2折角平分线的方法,那必将是顺理成章、顺水推舟。
如果如图2这样折叠△ABC呢,折痕AD具有什么特点?
折痕AD平分∠BAC,称线段AD为△ABC的角平分线。
给出三角形角平分线的定义,并问:一个三角形有几条角平分线?
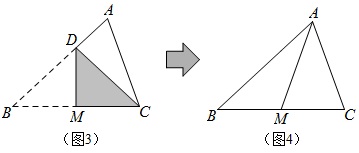
(3)该让中线登场了,高线小学已学,角平分线老师折好让学生找特点,那么中线应该换一种方法呈现了,让学生按要求折纸。
请同学们将三角形折叠,使折痕将原三角形分成两个三角形,且这两个三角形的面积相等。
学生如果有困难,可以如下启发:
①折痕一定要过三角形的一个顶点;
②折痕的另一个端点必须是这个顶点对边的中点。
也就是图3,图4的折叠方法。
给出三角形中线的定义,并问:一个三角形有几条中线?
2、画三角形的主要线段
(1)用三角板和量角器画一个三角形的三条角平分线,你发现了什么?
发现三角形的三条角平分线交于一点。
(2)用三角板画一个三角形的三条中线,你发现了什么?
发现三角形的三条中线交于一点。
(3)用三角板分别画锐角三角形、直角三角形、钝角三角形的三条高线,你发现了什么?
发现锐角三角形的三条高线都在形内,直角三角形斜边上的高线在形内,另两条高线在边上,钝角三角形最大边上的高线在形内,其余高线在形外,任何三角形三条高线所在的直线交于一点。
这里出现第一次教学难点—-画钝角三角形的高,学生的错误画法常有以下2种:
突破难点的方法可以与学生一起回忆高线的定义:三角形一边上的高是这边对角顶点到这边的垂线段。
问:AB上的高必须过哪个顶点?必须垂直于哪边?
3、与三角形主要线段有关的几个重要结论
为了辨清概念,为以后解决问题积累经验,有必要和学生一起得出以下结论:
(1)三角形的中线、高线和角平分线的共同之处是 。(都是线段,所在直线都交于一点)
(2)三角形的高线与中线、角平分线的位置上不同点是 。(高有可能在三角形外,而中线、角平分线一定在形内)
(3)三角形的中线平分三角形的 。(一条边,面积)
得出这条性质前可以先提出下面的问题:
若AD是△ABC的中线,请写出与AD有关的结论。
(BD=CD=\frac{1}{2}BC,S_{\triangle{ABD}}=S_{\triangle{BDC}}=\frac{1}{2}S_{\triangle{ABC}}
(4)三角形的角平分线所在的直线可以看作一个内角的 。(对称轴)
得出这条性质前可以先提出下面的问题:
如图2,折叠△ABC使点C落在AB上,折痕AD可以看作什么?(角平分线,∠BAC的对称轴)
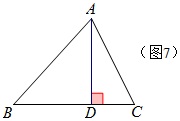
(5)如图7,AD是△ABC的高,写出与AD有关的等量关系。
∠ADB=∠ADC=90°,∠B+∠BAD=90°,∠C+∠DAC=90°,
S_{\triangle{ABC}}=\frac{1}{2}\times{BC}\times{AD}。
4、上述结论的应用
(1)角度的计算
例1 书本例2
本题是这节课的难点之二,突破难点的方法是分析法分析思路(与分析法相反的是综合法)。
提问:
①已知80°和40°可以求哪个角?由AE是角平分线可以求哪些角?AD是高线又可以求哪些角?
②要求∠DAE可以通过∠DAC与∠EAC的差计算,你还有什么方法?(至少还有3种方法)
变式:
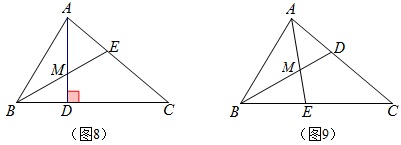
①如图8,若将角平分线AE改为角平分线BE,BE和AD交于M,如何求∠AMB的度数?
②如图9,若将高线AD改为角平分线BD,BD和AE交于M,如何求∠AMB的度数?
③原题中∠BAC=80°,∠C=40°改为∠B=α,∠C=β(α>β),其他条件不变,求∠DAE的度数。
(2)角平分线当对称轴
例2 如图10,AD是△ABC的角平分线,AB=5,AC=3,请说明:BD-DC<2.
用提问形式启发:
①我们已经学过的几何中线段的不等量关系有哪些?(三角形三边的关系)
②BD和CD在同一直线上,必须转化为什么?(转化为一个三角形中)
③转化的方法是什么?(轴对称)
解:如图11,将△ACD沿AD进行轴对称变换,点C的对应点为C’,因为AD是角平分线,所以点C’在AB上,且BC’=5-3=2,
所以BD-DC=BD-DC'<BC’=2.
角平分线当对称轴使用,是今后解题的经验,这节课是绝佳的机会。
(3)中线平分三角形的面积
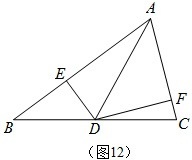
例3 如图12,△ABC中AD是中线,DE⊥AB于E,DF⊥AC于F,AB=6,AC=4,DF=3,求DE。
启发:
①中线具有什么性质?(平分边和面积)
②垂线段常常和什么联系在一起?(面积)
③你能写出哪4条线段的一个怎样的数量关系?(\frac{1}{2}\times{AB}\times{DE}=\frac{1}{2}\times{AC}\times{DF})
解:略。
与三角形主要线段有关的数学问题很多,由于时间关系,不能面面俱到了。很喜欢下面问题,可以作为课后练习。
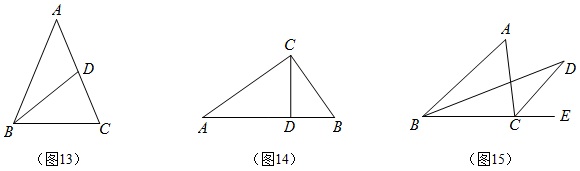
备用题1 如图13,AB=AC,中线BD将△ABC的周长分成12cm和9cm两部分,求BC长。
备用题2 如图14,已知△ABC中,∠ACB=90°,AC=8,BC=6,AB=10,求高CD的长。
备用题3 如图15,△ABC中,∠ABC和外角∠ACE的平分线交于点D,∠A=α,求∠D。
5、小结
小结有几种方法。
(1)知识点罗列。
(2)知识点和所用到的思想方法罗列。
(3)叫学生谈收获或体会。
(4)以问题形式代替小结。
(5)以上方法并用。
我采用的小结方法是:
1、今天我们学习了三角形的角平分线、中线和高线,我们来回顾这些三角形的主要线段的一些数量关系。
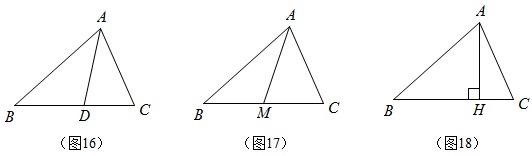
2、如图16,AD是△ABC的角平分线,\angle{BAD}=\angle =\frac{1}{2}\angle 。
\angle{C}-\angle{B}=\angle –\angle 。(利用外角的性质或轴对称)
3、如图17,AM是△ABC的中线,你能得出什么数量关系?(BM=MC,△ABM和△ACM面积相等,△ABM和△ACM的周长差=|AB-AC|)
4、如图18,AH是△ABC的高线,你能得出什么数量关系?(除角的关系外还有面积关系S_{\triangle{ABC}}=\frac{1}{2}\times{BC}\times{AH})
这样的小结方法是上述方法中(1)和(4)并用。

学习了
黄老师的设计很独特,学习了恩师