宁波市第七中学1706班
黄紫琳
(注:此文获江东区首届学生数学小论文一等奖)
学习数学一个重要的任务是解题,解题能帮助我们开拓思维,大胆创新,培养我们严谨的数学思发散思维和创造能,使我们具有良好的数学素养。解题思路清晰是解题的一大关键所在,所谓思路清晰,就是审题后从已知条件出发得出各种结论,或从结论出发探求得出这个结论所需要的条件,逐渐沟通条件和结论的联系。
解题方法因分析的思路不同而别,方法越多说明思维越灵活,知识掌握得越牢固、越熟练。数学题的一题多解并不少见,可就是解题的多种途径不容易被发现,人们常常会想不到许多解题方法,使之解题方法单一。下面以一道简单的与圆有关的几何题为例,说明一题多解是如何实现的。
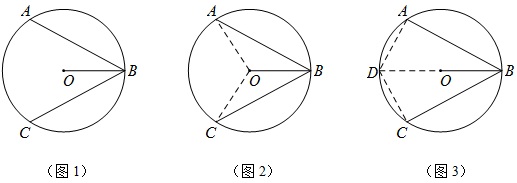
题目:如图1,⊙O中AB,BC是弦,AB=BC,求证:OB平分∠ABC。
这道题我首先想到构造全等来证明∠ABO=∠CBO,原来没有的全等三角形是如何被构造出来的呢?我想到了利用半径构造全等三角形。
解法1
如图2,连结AO,CO,
∵AO=CO,AB=CB,OB=OB,
∴△ABO≌△CBO,
∴∠ABO=∠CBO。
圆的的半径处处相等,这是一个极有用的性质,本方法即用半径相等构造了全等三角形。其实利用直径也可以构造全等三角形,于是便有如下解法。
解法2
如图3,作直径BD,连结AD和CD,
∵∠A=∠C=Rt∠,AB=CB,DB=DB,
∴△ABD≌△CBD,
∴∠ABO=∠CBO。
本方法采用了定理“直径所对的圆周角是直角”,由于直径的这个作用,所以常有“见直径找直角”之说。
圆中还有一条非常有用的定理:在同圆或等圆中,两条弧、两条弧所对的弦、两个弧所对的圆心角、两条弦心距,这四组量中若有一组量相等,那么其余各组量对应相等。这个定理就能实现不同量之间的转化,我们称之为“等对等定理”。
如果我们将本题条件AB=CB转化为\stackrel\frown{AB}=\stackrel\frown{BC},即可利用弧的关系来证明角的关系。
解法3
如图4,作直径BD,
∵AB=CB,
∴\stackrel\frown{AB}=\stackrel\frown{BC},
又∵\stackrel\frown{DAB}=\stackrel\frown{DCB},
∴\stackrel\frown{AD}=\stackrel\frown{CD},
∴∠ABO=∠CBO。
弦的关系可以转化为弧、圆心角或弦心距的关系,所以说“等对等定理”是给我们转化用的。我们还可以想到利用定理“在角的内部,到角两边的距离相等的点在角平分线上”来解决本题。
解法4
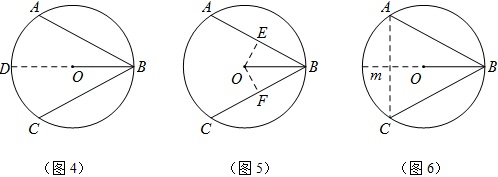
如图5,作弦心距OE,OF,
∵AB=CB,
∴OE=OF(等对等定理),
∴∠ABO=∠CBO。
你看,弦心距沟通了弦和角之间的关系,可见弦心距是沟通关系的“桥梁”。我还想,学习了三角函数后,能不能发挥一下作用呢?经过思考方法找到了。
解法5
如图3,作直径BD,连结AD和CD,
∴∠A=∠C=Rt∠,
∵cos\angle{ABD}=\frac{AB}{DB},cos\angle{CBD}=\frac{CB}{DB},AB=CB,
∴cos\angle{ABD}=cos\angle{CBD},,
即∠ABO=∠CBO。
此法用三角函数关系代替的全等三角形,所以三角函数不失为沟通边角关系的妙法。
还有其他方法吗?全等三角形用了,转化到弧解决用了,弦心距用了,三角函数用了,这些方法以外还有吗?连结AC是不是可以解决问题呢?许久,第6种方法诞生了。
解法6
如图6,连结AC,作AC的中垂线m,
∴直线m过圆心O(弦的中垂线必过圆心),
∵AB=CB,
∴直线m过点B(到线段两个端点距离相等的点在这条线段的中垂线上),
∴∠ABO=∠CBO(三线合一)。
本方法弦的中垂线将两个定理用到了恰到好处,如果在图6中是延长BO,或作AC的弦心距,都难以进行推理,这就是为什么选用中垂线推理的缘故。
一道如此简单的题,居然找到了6中解法,实在是高兴啊!我想,应该还有更多的方法吧,聪明的你是否心动了,也想挑战一下自己?
数学好玩,解题锻炼意志品质,提高多种能力。愿我们在数学解题中,尤其是一题多解中,发挥我们的聪明才智,发挥我们的想象力和创造力,坚持不懈地对每个数学问题进行深入研究,找到解决问题的多种方法,比较各种方法的优劣,促进对问题的研究,善于发现问题、提出问题,提高分析问题和解决问题的能力,锻炼我们良好的数学品质。
基本上园的所有性质都用个遍,真的不错!
真棒?
太棒了