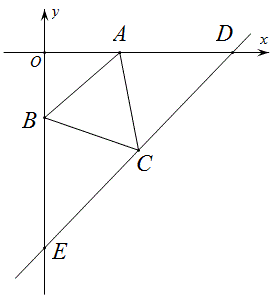
问题:如图,正三角形ABC中,A(4,0),B(0,-2\sqrt{3}),D(10,0),求直线DC的解析式。
请看下面四种解法,各有巧妙不同,运算量大小不一,你更喜欢哪种?
解法1:
如图,作垂线CF,CG,设AF=x,CF=y,那么CG=x+4,BG=y-2\sqrt{3},
可得方程组:\begin{cases} x ^2+ y^2 =28\\ (x+4)^2+(y-2\sqrt{3})^2 = 28 \end{cases},解之\begin{cases} x=1\\ y=3\sqrt{3} \end{cases},
所以C(5,-3\sqrt{3}),
所以直线DC的解析式为y=\frac{3}{5}\sqrt{3}x-6\sqrt{3}.
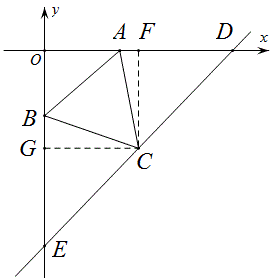
解法2:
作正△OBH,直线HC交x轴于J,易证OJ=2,所以直线HJ的解析式为y=-\sqrt{3}x+2\sqrt{3}.
同理,在第2个图中GI的解析式是y=-\frac{1}{3}\sqrt{3}x-\frac{4}{3}\sqrt{3}.
这样直线HJ和直线GI的交点就是C(5,-3\sqrt{3}),
所以直线DC的解析式为y=\frac{3}{5}\sqrt{3}x-6\sqrt{3}.
本方法其实就是找C点关于A和B的两条轨迹。
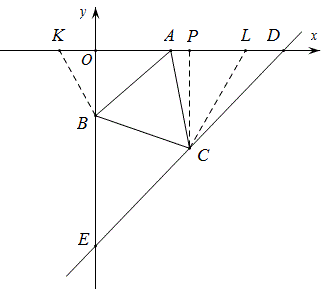
解法3:
如图,在x轴上找点K,L,使得∠AKB=∠ALC=60°,作CP⊥x轴于P。
易证△ABK≌△CLA,所以AL=BK=4,CL=AK=6,
故PL=3,PC=3\sqrt{3},
C(5,-3\sqrt{3}),
所以直线DC的解析式为y=\frac{3}{5}\sqrt{3}x-6\sqrt{3}.
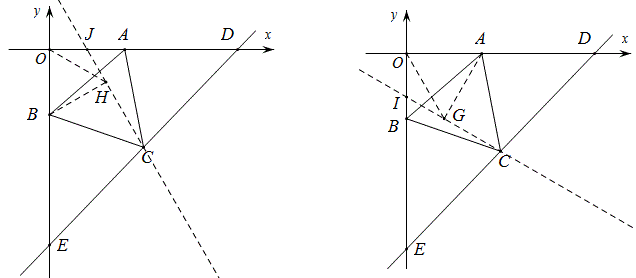
解法4:
如图,延长AC至M,使CM=AC,连结BM,作MN⊥y轴于N,
易证△AOB∽△BMN,故MN=6,
设DE与MN交于Q(图中没标出),∴△MQC≌△ADC,故MQ=AD=6,
所以N,Q重合,∵N在y轴上又在直线DC上,∴N,E重合,∴E(0,-6\sqrt{3}),
所以直线DC的解析式为y=\frac{3}{5}\sqrt{3}x-6\sqrt{3}.
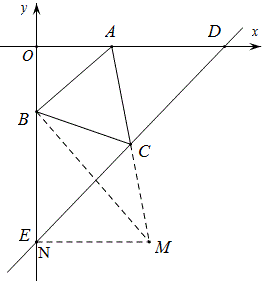
方法4的M点求出来了,还可以用AM的中点公式
跟着师父学习,这方法2和上次那题前后打通,好多有意思的结论。佩服。
方法2很神奇,佩服。里面蕴含着比值根号3为定值的这结论。