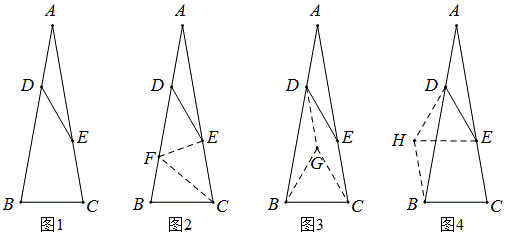
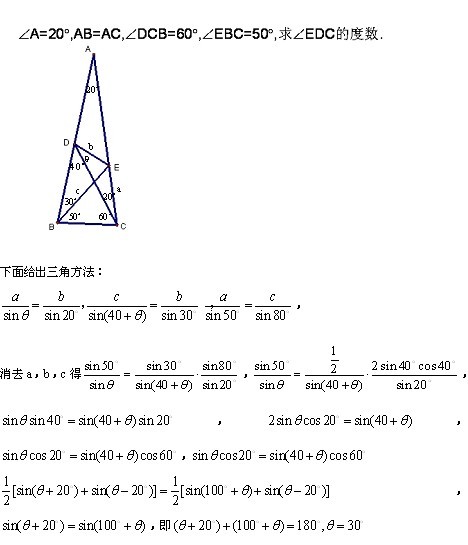
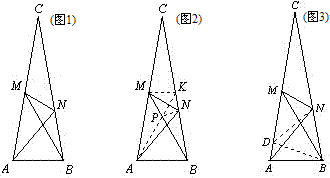问题:如图1,△ABC中,AB=AC,D,E分别在AB,AC上,且AD=DE=EC=BC,求证:∠A=20°.
解法1:如图2
作∠ACB的角平分线CF,连EF,那么△BCF≌△ECF,设∠A=x°,于是∠B=∠FEC=90-\frac{1}{2}x,
∠DEF=180-x-(90-\frac{1}{2}x)=90-\frac{1}{2}x=∠FEC.
∴△DEF≌△CEF,∴∠BFC=∠EFC=∠EFD=60°,
在△BFC中,∵一个角为60°,另两个角是2倍关系,∴∠B=80°,∴∠A=20°.
解法2:如图3
作菱形DECG,连BG,则BC=GC,∵AB=AC,AD=CE,∴BD=AE,
∴△BCF≌△ECF,∴BG=DE=BC=GC,∴△GBC为正三角形,不难求出∠A=20°.
解法3: 如图4
作菱形HBCE,连AH,则HE=DH,∵AB=AC,AD=CE,∴BD=AE,
∴△ADE≌△DHB,∴DH=DE=BC=HE,∴△DHE为正三角形,不难求出∠A=20°.
解法4:如图3
设∠A=x°,那么∠GCB=\dfrac{180-x}{2}-x=90-\dfrac{3}{2}x,
∠GBC=\dfrac{180-(90-\frac{3}{2}x)}{2}-x=45+\dfrac{3}{4}x,
∠ABG=\dfrac{180-x}{2}-(45+\dfrac{3}{4}x)=45-\dfrac{5}{4}x,
∵(BG-DG)^2=(BG-DG)(BG-GC)\ge0
∴由大边对大角得:[x-(45-\dfrac{5}{4}x)][(90-\dfrac{3}{2}x)-(45+\dfrac{3}{4}x)]\ge0
化简得:(\dfrac{9}{4}x-45)(45-\dfrac{9}{4}x)\ge0
∴\dfrac{9}{4}x-45=0,x=20.
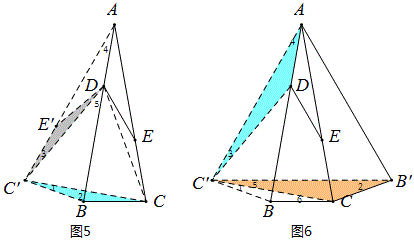
解法5:如图5
反射△ABC,∵CC’⊥AB,∴∠1=90°-∠2,∠3=\frac{1}{2}∠4=90°-∠2,
∴∠1=∠3,∴△CC’B≌△DC’E’,∴△DCC’是正三角形,∴∠5=30°,
∵∠5=∠3+∠4=3∠3,∴∠4=20°.
解法6:如图6
将三角形左右反射,∠1=∠6=∠5=∠3,∠4=2∠3=∠2,∴△CC’B’≌△AC’B’,
∴△AC’B’是正三角形,∴∠BAC=20°.
顶角为20°的等腰三角形具有许多性质,举例如下:
例1 如图3,可以将三角形分割成3个、4个、5个、n个(n>2的整数)等腰三角形。
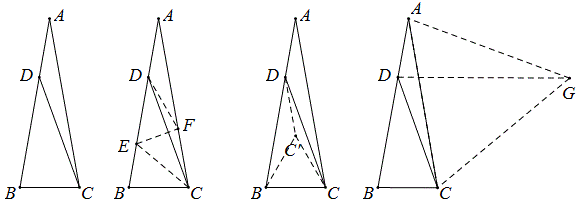
例2 如图AB=AC,∠A=20°,AD=BC,求∠BDC。
解法1:类似上面图2,不难计算∠BDC=30°.
解法2:作正三角形BCC’,连DC’,不难证明四边形ADC’C是等腰梯形,
所以C’D=C’B=C’C,即C’是△DBC的外心,所以∠BDC=∠BC’C÷2=30°.
也可以连AC’,证明△AC’C≌△ADC,直接算出∠ADC=∠AC’D=150°,∴∠BDC=30°.
解法3:作正三角形ACG,连DG,这样△ADG≌△ABC,于是△ADG和△DCG均为等腰三角形,且顶角为20°和40°,于是不难求出∠BDC=30°.
例3 如图1,△ABC中,∠C=20°,AC=BC,M,N分别在AC,BC上,∠MBA=60°,∠NAB=50°,求∠NMB.
方法1
如图2,作MK∥AB交BC于K,连结AK交BM于P,连结PN。
则△ABP和△MKP均为正三角形,
易证PB=AB=BN,故∠NPB=(180-20)÷2=80°,∠KPN=120-80=40=∠PKN,
所以NP=NK,所以△PMN≌△KMN,所以∠NMB=30°.
方法2:如图3
方法3: