想加快解几何题的速度,就要牢记常见的几何命题的图形、条件和结论。我把它叫做“几何基本模式”。
“基本模式”虽然不是定理,虽然不能在证明过程中直接应用,但其作用不亚于定理,至少我们可以在填空题、选择题中加以应用,还可以运用它进行问题的分析,作为推理的依据,看清解题思路,加快思维速度。几何基本模式就是我们解题的经验,模式记得越多经验就越多。下面举例一一加以说明。
一、角平分线的基本模式
1、同旁内角的角平分线互相垂直
如图,直线a∥直线b,AC和BC是一对同旁内角的角平分线,那么AC⊥BC.
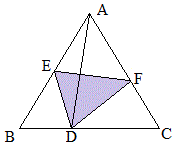
例1 如图平行四边形ABCD中,四个内角的角平分线围成一个四边形EFGH,请判别这个四边形是什么特殊的四边形.
解:由本几何模式可知,四边形EFGH是矩形.
2、邻补角的角平分线互相垂直
如图,OD、OE分别平分∠AOC、∠BOC,那么OD⊥OE.
例2 (天津2012)已知一个矩形纸片OACB,将该纸片放置在平面直角坐标洗中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
解决以上问题这要用到PO⊥PQ的结论。利用这个结论我们还可以证明CC’∥PO.
例3 如图,一张平行四边形纸片ABCD,E,F,G,H分别在四条边上,分别沿FG,GE,EH,HF将三角形AFG,BGE,CEH,DHF折叠,结果A和B都落在EF上的A’, C和D都落在EF上的C’,得到一个信封EHFG,若AD=10,AB=6,求EF的长。
解:由上述基本模式可知,四边形EHFG为矩形,所以EF=GH=AD=10.
3、平行线+角平分线\Rightarrow等腰三角形
如图,OC平分∠AOB,D、E分别在AO、CO上,DE∥OB,那么DE=OD.反之亦然。
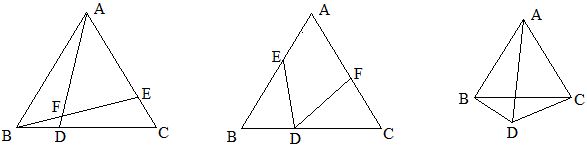
例4 如图DB、DC分别平分△ABC的内角,过D点作EF∥BC交AB、AC于E、F,AB+AC=12,求△AEF的周长.
解:利用这个基本模式可得:ED=EB,FD=FC,所以△AEF的周长=AB+AC=12.
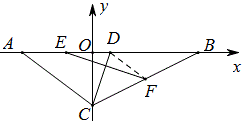
例5 如图,已知A(-8,0),B(12,0),C(0,-6),D(2,0),E在x轴负半轴,F在BC上,EF被CD垂直平分,求E,F的坐标。
解:连DF,那么CD平分∠ADF,又△ACD为等腰三角形,上面是模式告诉我们:角平分线、平行线和等腰三角形三个条件中,知其二推其余。故DF∥AC,所以DF是中位线,DF=AC/2=5=DE,这样就不难求得E(-3,0),F(6,-3).
二、全等三角形的基本模式
1、角平分线+垂线\Rightarrow全等三角形
如图,D是∠CAB的边AC上一点,过D作∠CAB的平分线的垂线于F,交AB于E,那么△AFD≌△AFE。
例6 如图,△ABC的周长为8,BF、CG分别平分外角∠ABE和∠ACD,过A点作BF、CG的垂线,垂足为M、N,求MN的长。
根据基本模式,可以延长AM、AN交直线BC于P、Q,由基本模式的结论可知△AMB≌△PMB及△ANC≌△QNC,所以M、N是AP、AQ的中点,所以MN=PQ/2=8÷2=4。
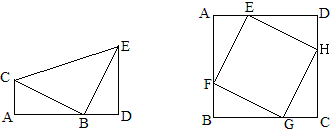
2、两个全等的直角三角形一横一竖放\Rightarrow等腰直角三角形
如图1,△BCE是等腰直角三角形,∠A=∠D=90°,A,D,B共线,那么△ABC≌△DEB。反之亦然。
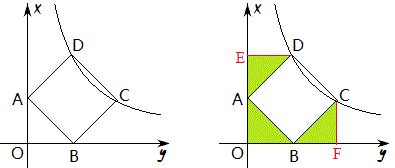
如图2,正方形ABCD和正方形EFGH,那么四个直角三角形全等。反之亦然。
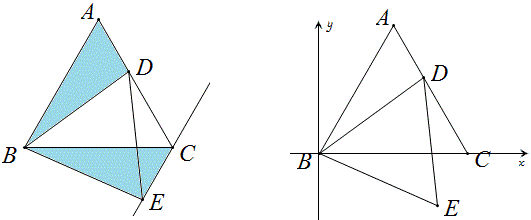
例7 如图,正方形ABCD中,A,B在坐标轴上,C,D在反比例\frac{k}{x}图象的第一象限分支上,求证:OA=OB.
解:如图作坐标轴的垂线,得到三个直角三角形全等。设OA=a,OB=b,那么D(a,a+b),C(a+b,b),所以a(a+b)=b(a+b),a=b。
3、SSA基本模式
定义:我们把两个三角形满足两边及其中一边的对角对应相等的现象叫做“SSA”。
SSA有以下两条性质:
1.有两边和其中一边的对角对应相等的两个三角形可能全等,可能不全等。(所以不能利用“SSA”判定两个三角形全等)
2.有两边和其中一边的对角对应相等的两个三角形如果不全等,那么它们的面积相差一个等腰三角形。
例8 如图,已知△ABC和△A’B’C’中,使AB= A’B’=8cm,AC= A’C’=5cm,∠B=∠B’=30°, 如果△ABC和△A’B’C’不全等,求它们的面积之差是多少平方厘米。
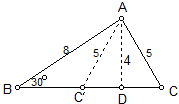
解:由上面性质2可知,如果把这两个三角形重叠起来,就相差一个等腰三角形(如图)。
其中A与A’重合,B 与B’重合,设C’落在BC上,作高AD,那么由几何性质知AD=4,CD=3,S△ACC’=12,此即为问题的解。
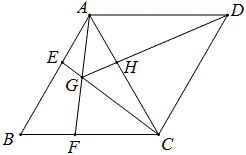
例9 如图四边形ABCD中,AD平分∠BAC,∠B+∠C=180°,求证:BD=CD。
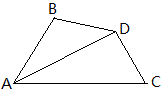
图中的两个三角形有三对元素相等,但却不全等,这是因为“边边角”的缘故。于是可以用割补法,添出如下图的辅助线。
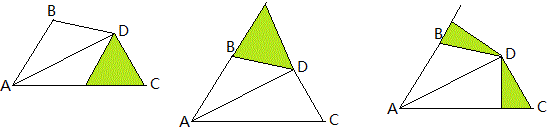
方法1、补上一个等腰三角形;方法2、割去一个等腰三角形;方法3、补上且割去半个等腰三角形。
三、特殊三角形中的基本模式
1、等边三角形中的基本模式
(1)一个等边三角形
①如图在正三角形ABC中,D、E分别在BC、AC上,BD=CE,BE,AD交于F,那么图中有2对全等三角形和4对相似三角形(不全等),且有∠AFE=60°。
②如图在正三角形ABC中,D、E、F分别在BC、AB、AC上,∠EDF=60°,那么图中的两个小三角形相似。
③如图D在正三角形ABC外,∠BDC=120°,那么AD=BD+CD,且AD平分∠BDC。
例10 如图,正三角形ABC中,D、E分别在BC、AC上,AE=CD=6,AD=9,求E到AD的距离。
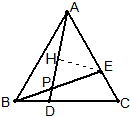 分析:先证△ABD≌△BCE,后证△APE∽△BAE,还有∠APE=60°,再由AE^2=EP\times{EB}算出EP的长,即可知道EH的长。
分析:先证△ABD≌△BCE,后证△APE∽△BAE,还有∠APE=60°,再由AE^2=EP\times{EB}算出EP的长,即可知道EH的长。
例11 如图在正三角形ABC中,D、E、F分别在BC、AB、AC上,沿EF折叠,A落在D,如果BD=3,CD=5,求AE的长。
解:由上面的几何模式②可知△BED∽△CDF,设AE=x,CF=y,那么
\dfrac{8-x}{5}=\dfrac{3}{y}=\dfrac{x}{8-y},解之x=\dfrac{49}{13}。
例12 如图菱形ABCD中,AB=AC,点E,F在AB,BC上,AE=BF,AF,CE交于G,GD和AC交于H,则下列结论中成立的有 个。
①△ABF≌△CAE;②∠AGD=60°;③DG=AG+GC;④AD^2=DH\times{DG};⑤△ABF≌△DAH。
由以上所列模式,不难证明5个结论均成立。
(2)两个等边三角形
有公共顶点的两个正三角形能组成一对全等三角形。
例13 边长为4的正三角形ABC如图放置在直角坐标系中,又正三角形BDE的顶点D在直线AC上移动,E在BD下方,那么E点经过的路径的解析式是 。
解:根据基本模式知直线CE与x轴的夹角始终为60°,故解析式是y=\sqrt{3}x-4\sqrt{3}。
2、直角三角形中的基本模式
作直角三角形ABC斜边AB上的高CD,得到的两个△ACD和△BCD与原三角形相似,我们称这个几何基本图形为母子三角形。
我们还可以得出母子三角形的另外几条结论:有两对锐角相等,有4对锐角互余,
CD^2=AD\times{BD},AC^2=AD\times{AB},CB^2=AB\times{BD}.
例14 如图,在Rt△ABC中,∠ABC=90°,BA=BC=4.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于的直线相交于点G,连接DF.求四边形ADEF的周长.
由已知,DB=2,CD=2\sqrt{5},由上面的模式,∠GBA=∠DCB,BD^2=DE\times{DC},
所以DE=\dfrac{2\sqrt{5}}{5},又易证△ABG≌△BCD,故AG=DB=AD=2,
由△AFG∽△CFB,所以\dfrac{AF}{FC}=\dfrac{AG}{BC}\dfrac{GF}{FB}=\dfrac{1}{2},AF=\dfrac{4\sqrt{2}}{3},GF=\dfrac{2\sqrt{5}}{3},
EF=GB-GF-EB=2\sqrt{5}-\dfrac{2\sqrt{5}}{3}-\dfrac{4\sqrt{5}}{5}=\dfrac{8\sqrt{5}}{15}.
所以四边形ADEF的周长=2+\dfrac{4\sqrt{2}}{3}+\dfrac{8\sqrt{5}}{15}+\dfrac{2\sqrt{5}}{5}=2+\dfrac{4\sqrt{2}}{3}+\dfrac{14\sqrt{5}}{15}.
3、等腰三角形中的基本模式
(1)腰上的高与底边的夹角=顶角的一半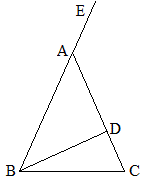
(2)顶角的外角=底角的2倍
如图,等腰三角形ABC中,AB=AC,延长BA至E,BD是高,那么
①∠DBC=\frac{1}{2}∠BAC;②∠EAC=2∠C。反之亦然。
(3)黄金三角形
一个内角为36°的等腰三角形称为黄金三角形,黄金三角形一定可以分割成2个黄金三角形。腰与底边之比成黄金比。
请参见文章《36°之美》。
4、等腰直角三角形中的基本模式
(1)等腰直角三角形中的直角
(2)等腰直角三角形中的45°角
如图等腰直角三角形ABC中,AB=AC,
①若M是BC的中点,D在AB上,E在AC上,∠DME=Rt∠,那么△ADM≌△CEM,从而AD=CE,MD=ME,四边形ADME的面积等于△ABC面积的一半……反之亦然。
②D、E分别在BC上,∠DAE=45°,那么BD^2+EC^2=DE^2,△ABE∽△ACD。反之亦然。
例15 如图,B是双曲线y=\dfrac{1}{2x}第一象限上的动点,作BC⊥x轴,BA⊥y轴,交直线y=-x+1于D、E,求证:∠DOE=45°.
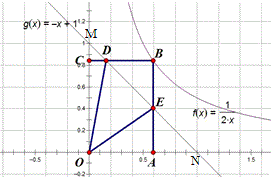
解法1:
∵CM=1-b=CD,AN=1-a=AE,BE=DB=a+b-1 ,
∴DE^2=MD^2+EN^2,将△OEN绕O点逆时针旋转90°可得证。
解法2:
DN=\sqrt{2}y_B, EM=\sqrt{2}x_B, DN\cdot{EM}=2x_B\cdot{y_B}=1=OM\cdot{ON},
得△MOE∽△DNO,∠ODN=∠MOE,∠DOE=∠OMN=45°.
续文请点击:《几何基本模式(续)》
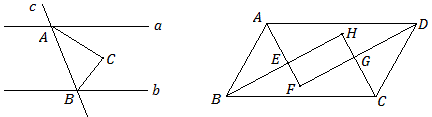
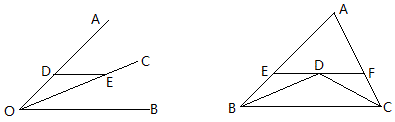
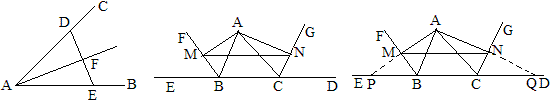
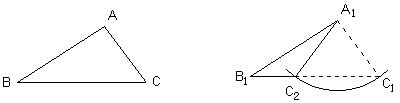
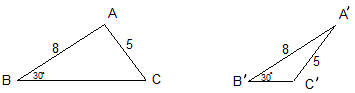
谢谢黄老师!
非常期待
很漂亮,黄老师把这些系统总结出来,很期待续文。