四、四边形中的基本模式
1、正方形
(1)正方形中的垂直线段
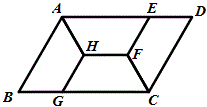
如图,在正方形ABCD中,EF⊥GH,那么EF=GH,反之亦然
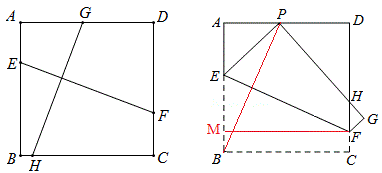
例16 如图所示,现有一张边长为7的正方形纸片ABCD,点P为正方形AD边上的一点,AP=3,将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,求FG的长。
解:连BP,作FM⊥AB于M,由上模式,因为BP⊥EF,所以△ABP≌△MFE,所以ME=AP=3,
设GF=CF=MB=x,那么EP=EB=3+x,AE=4-x,由△AEP中的勾股定理得,(3+x)^2=(4-x)^2+3^2,
解得x=\frac{8}{7}。
注:连结PF利用两个直角三角形的公共斜边,解法更为简单。
(2)正方形内45°角
如图,正方形ABCD中,E,F分别在DC,BC上,∠EAF=45°,那么有以下一些结论:
(1)BE+DF=EF;(2)△CEF的周长=2AB;(3)将△ABE和△ADF分别沿AE,AF折叠,B,D会落在EF上的同一点。
反之也然。
例17 如图所示,现有一张边长为7的正方形纸片ABCD,点P为正方形AD边上的一个动点,将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,问△DPH的周长是否变化?若不变,请求 出周长;若变化,请说明理由。
解:连BP,BH,作BQ⊥PH于Q,易证△APB≌△QPB,△QBH≌△CBH,这样就得到本模式,所以△DPH的周长不变化,周长为2AB=14.
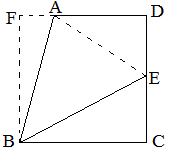
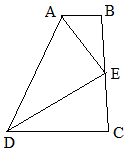
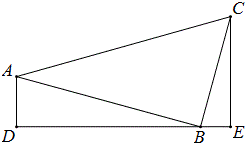
例18 如图,直角梯形ABCD中,∠C=∠D=90°,BC=CD=4,AD=3,E在CD上,∠ABE=45°,求CE的长。
解:补全图形为正方形FBCD,则为本模式,设CE=x,那么DE=4-x,AE=1+x,由3^2+(4-x)^2=(1+x)^2,
解得x=2.6.
2、对角线夹角为60°的矩形
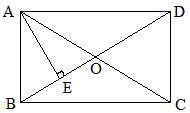
如图,矩形ABCD中,AC、BD交于O,AE⊥BD于E,那么下列论断中
①AB=AO;②∠AOB=60°;③E是BO的中点;④AB:BC:AC=1:\sqrt{3}:2;⑤∠ADB=30°;⑥AO:AD=1:\sqrt{3}.
已知其一必知其余。
例19 如图,矩形ABCD中,AC、BD交于O,AE⊥BD于E,E是BO的中点,∠BCD的平分线交EA延长线于F,交AD于G,已知AB=6,求FG的长。
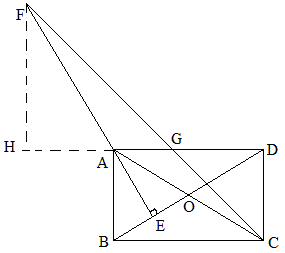
解:由基本模式得知,△AOB为正三角形,易证∠ACF=∠AFC=15°,∴AF=AC=2AB=12,∠FGA=45°,
作FH⊥DA交延长线于H,那么∠FAH=60°,∴FH=\dfrac{\sqrt{3}}{2}AF=6\sqrt{3},
∴FG=\sqrt{2}FH=6\sqrt{6}.
3、内角为60°的菱形
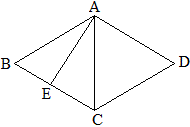
这是两个全等的正三角形拼成的菱形,若菱形ABCD满足下列条件之一,则必满足其余。
①AB=AC,②对角线之比为1:\sqrt{3},③高AE平分BC,④在BC上任取一点M,作∠MAN=60°交CD于N,则△AMN是正三角形。
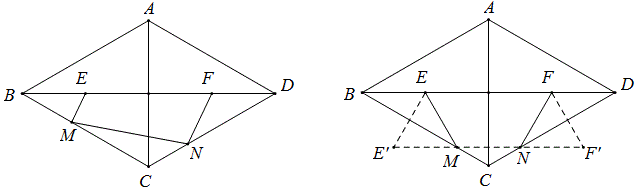
例20 菱形ABCD中,BD=\sqrt{3}AC,BD,AC交于O,BO,DO的中点分别为E,F,M,N是BC,DC上的动点,若EF=6,求四边形EFNM周长的最小值。
解:由基本模式得∠DBC=30°,作轴对称点E’和F’,那么E’F’=2BE+MN=6+3=9,所以四边形EFNM的周长的最小值为9+6=15.
4、3个全等的等边三角形拼成的等腰梯形
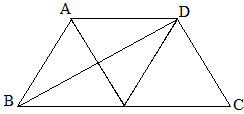
如图梯形ABCD中,AD∥BC,AB=DC,对于下列结论中:①∠C=60°;②BD⊥DC;③BD平分∠ABC;④BC=2AB;⑤AB=AD;⑥周长=5AD。已知两个便知其余。
例21 三个全等的正三角形拼成等腰梯形叫做正梯形,(1)正梯形有哪些性质?(写出6条)(2)写出3条正梯形的判定方法;(3)如图是4个全等的等腰梯形拼成的平行四边形,运用你写出的正梯形的判定方法求证:这样的等腰梯形是正梯形;(4)若AD=12,求梯形的对角线是长。
解:(1)即为本模式的6个结论,当然还有更多的结论可以得出。
(2)6条结论中已知2条即可判断正梯形。如果一个等腰梯形的腰长等于较小的底边,一个内角等于120°,那么这个梯形是正梯形。
(3)由图形结构可以看出,这个梯形满足“一个等腰梯形的腰长等于较小的底边,一个内角等于120°”,所以它是正梯形。
(4)∵AD=12,∴GH=4,∴BH=4\sqrt{3}.
5、两底之和等于一腰的梯形
如图,梯形ABCD中,AB∥DC,E在BC上。以下5个结论:①AB+DC=AD;②E为BC中点;③AE平分∠BAD;④DE平分∠ADC;⑤∠AED=90°.已知其中2条性质,必知其余。
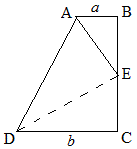
例22 梯形ABCD中,AB∥DC,∠B=90°,E是BC中点,AE平分∠BAD,AD=13,BC=12,求AE的长。
解:连DE,由本模式得∠AED=90°,DE平分∠ADC,AB+DC=AD。
所以△ABE∽△ECD,那么\begin{cases} a+b=13\\ ab=6^2 \end{cases}
∴a=4,b=9.
五、相似三角形中的基本模式
1、A字型;2、X型;3、不平行相似;4、两个公共
四种基本模式有如下关系:
对“两个公共”的基本模式特别说明:
有公共角和公共边的两个相似三角形叫做“两个公共”。两个公共具有两条重要性质:①公共边是同一直线两边的比例中项;②公共角所对的两边之比是相似比。
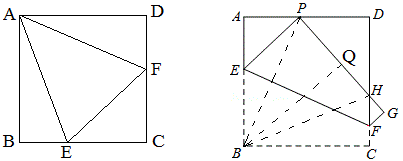
例23 如图,正三角形ABC中,D、E分别在BC、AC上,AE=CD=6,AD=9,求E到AD的距离。
解:由正三角形模式知△AEP∽△AEB,再由本模式得AE^2=EP\times{EB},求出PE=4,
又由正三角形模式知∠APE=60°,故EH=2\sqrt{3}.
例24 如图Rt△ABC中,∠BAC=Rt∠,D在CB延长线上,∠DAB=∠C,DB=4,BC=5,求AB的长.BC
解:由“两个公共”模式得AD^2=DB\times{DC},故AD=6,
再由“两个公共”模式的第二个结论得AB:AC=AD:DC=6:9=2:3,由勾股定理可求AB的长是\dfrac{10}{13}\sqrt{13}
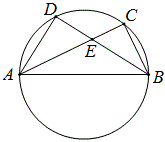
例24-2 如图,AB是直径,BC,AD是弦,BD平分∠ABC,AC与BD交于E,AE=6,AB=8,求tan∠CEB。
解:由∠DAE=∠CBE=∠DBA得△ADE∽△BDA,所以tan∠CEB=tan∠AED=\dfrac{AD}{DE}=\dfrac{AB}{AE}=\dfrac{8}{6}=\dfrac{4}{3}.
5、等边三角形外的120°角
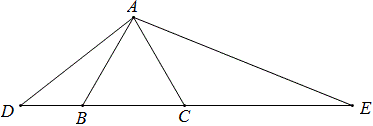
如图,△ABC是正三角形,D,E分别在CB,BC的延长线上,∠DAE=120°,那么图中有3对三角形相似,并有如下等式成立:
①AD^2=DB\times{DE};②AE^2=EC\times{ED};③BC^2=DB\times{CE};
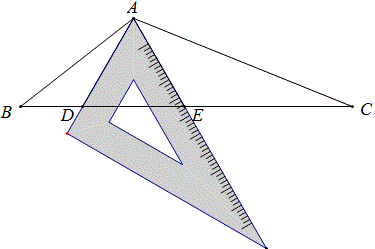
例25 如图,△ABC中,∠BAC=120°,AB=1,AC=2,一块含有60度的三角板的60°顶点与A重合,若三角板位于△ABC内部的三角形是正三角形,求这个正三角形的边长。(本题解答留给读者)
6、三个直角三角形
如图,△ABC中∠ABC=Rt∠,过B点任作直线DE,AD⊥DE,CE⊥DE,那么△ADB∽△BEC。
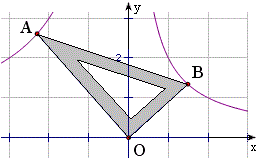
例26 如图,一块含30°角的三角板的直角顶点是坐标原点O,30°的顶点A在反比例函数\dfrac{m}{x}图象上,B在反比例函数\dfrac{2}{x}图象上,求m的值。
解:过A,B作x轴垂线,则得本模式,由相似三角形的性质可求m。(具体计算过程略)
7、三角形的内接矩形
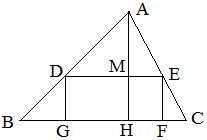
如图矩形DEFG内接于上进心ABC中,高AH交DE于M,那么△ADE∽△ABC,且\dfrac{AM}{AH}=\dfrac{DE}{BC}
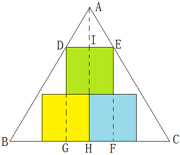
例27 正三角形ABC的边长为2,按如图设计在里面剪出三个最大的正方形,求正方形的边长。
解:设正方形的边长为x,按本模式得\dfrac{x}{2}=\dfrac{\sqrt{3}-2x}{\sqrt{3}},得x=\dfrac{8\sqrt{3}-6}{13}.
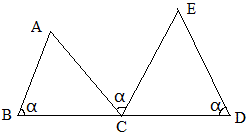
8、一线三等角
如图,B,C,D共线,三个角都是α,那么两个三角形相似。
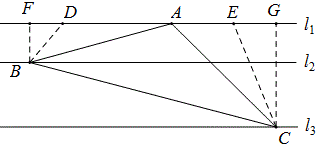
例28 如图,直线l_1、l_2、l_3相互平行,且l_1、l_2的距离为1,l_2、l_3的距离为2,等腰△ABC的三个顶点分别在三条平行线上,AB=AC,∠BAC=120°,则等腰△ABC的腰长是______________.
解:在l_1上取点D,E,使∠ADB=∠AEC=∠BAC=120°,由本模式△ABD≌△ACE,作BF⊥l_1,CG⊥l_1,不难求得AE=BD=\dfrac{2\sqrt{3}}{3},EG=\sqrt{3},
故AC=\sqrt{(\dfrac{5\sqrt{3}}{3})^2+3^2}=\dfrac{2\sqrt{39}}{3},
六、圆中的基本模式
1、圆内接等腰三角形;2、圆内接三角形的角平分线
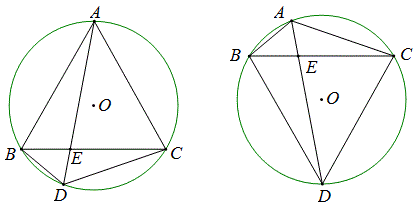
(1)如图,△ABC内接于圆O,D是圆上一点,AD交BC于E,如果AB=AC,那么图中有6对相似三角形,
AB^2=AC^2=AE\times{AD},DB\times{DC}=DE\times{DA}.
(2)如图,△ABC内接于圆O,D是圆上一点,AD交BC于E,如果AD平分∠BAC,那么图中有6对相似三角形,
BD^2=CD^2=DE\times{DA},AB\times{AC}=AE\times{AD}.
例29 如上图2,△ABC内接于圆O,D是圆上一点,AD交BC于E,如果AD平分∠BAC,AB=1,AC=2,AD=3,求BD。
解:由本模式,1×2=3×AE,得AE=\dfrac{2}{3},故BD^2=3\times(3-\dfrac{2}{3})=7,∴BD=\sqrt{7}.
3、圆内接梯形
圆内接梯形必为等腰梯形。
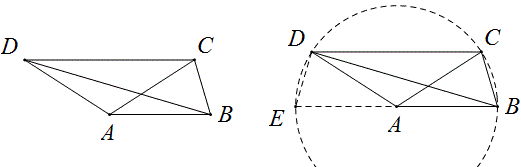
例30 如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则BD的长等于 。
解:过B,C,D三点作⊙A,延长BA交圆于E,连DE,那么四边形EBCD为等腰梯形,BE=4,DE=BC=1,在Rt△BDE中,BD=\sqrt{15}。
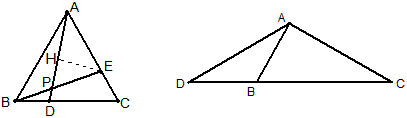
第一个正方形的结论反之不亦然。中考有考过,多种情况
请指出具体的问题@匿名
圆中的基本模式1、圆内接等腰三角形;2、圆内接三角形的角平分线
好像有点问题,
四月份的课上讲过了
三角形PDH周长不变是另外一个模式了,所以这里就不写了
黄老师,四、四边形中的基本模式
1)正方形中的垂直线段中的三角形PDH周长不变,好像没写
黄老师的博客让我受益良多,您生活、工作中的井井有条、细腻等优秀的品质,让我敬佩,也值得学习!
[latex]ax^2+bx+c=0[/latex]
$3^2+4^2=5^2$
无意中发现黄老师的博客 受益良多
我试一下公式输入 3^2+4^2=5^2
武学太极72式,数学黄氏108式。期待!