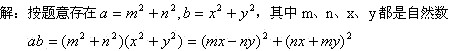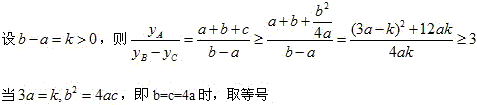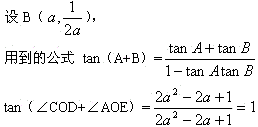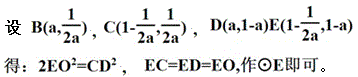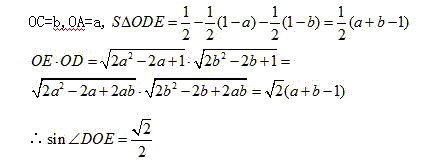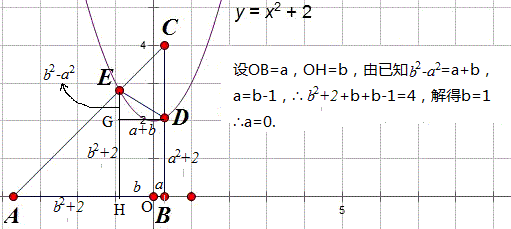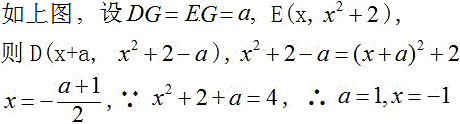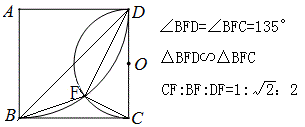前面已有4篇汇总:
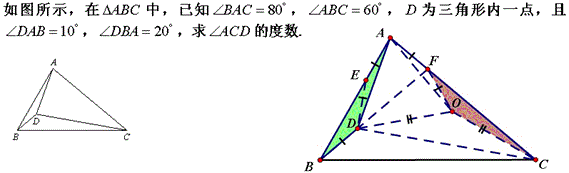
问题42
黄冈朱老师的解答:
延长BD交AC于F,作A关于BF的对称点O,AD的垂直平分线交AB于E点。
显然△BAF为顶角为20°的等腰三角形,且△ADO为正三角形,BD=DE=AE。
∠BAO=10°+60°=70°,∴∠FAO=80°-70°=10°。
△AED和△AFO均为底角为10°的等腰三角形,且AD=AO,所以两三角形全等,
于是AF=FO=AE=ED=BD。注意到∠FBC=60°-20°=40°=∠FCB,于是FB=FC。
又∠OFC=2×∠OAF=20°,FO=BD,FC=BF=AB,故△ABD≌△CFO,∴OC=AD=OA=OD。
于是∠AOD=60°=∠OAC+∠ACD+∠CDO=2×(∠ACO+∠DCO)=2×∠ACD,∴∠ACD=30°。
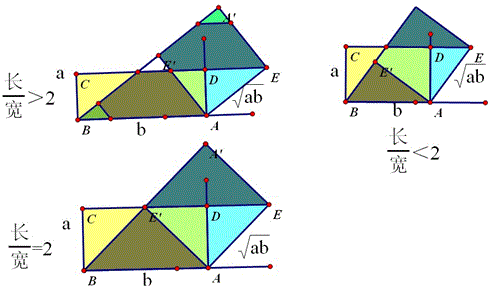
问题43(春晓–团老师提供)
求解:一个a乘b的长方形如何剪拼成正方形?
慈溪李先兵的解答:
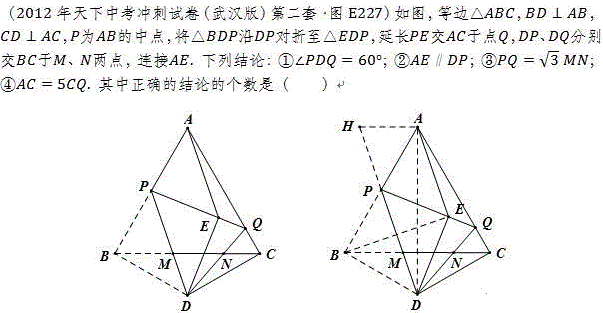
问题44(黄冈朱老师提供)
朱老师给出的答案是:
问题45(2012年10月24日樊贞慧提供)
猜想:在网格中如果√a和√b(a,b均是正整数)都是格点线段,那么√ab也是格点线段(所谓格点线段指的是两个端点均在格点上)。帮忙验证一下。
古林中学张利芳解答:
问题46(2012年10月30日星期二学生陈宇欣问黄伟建的题目)
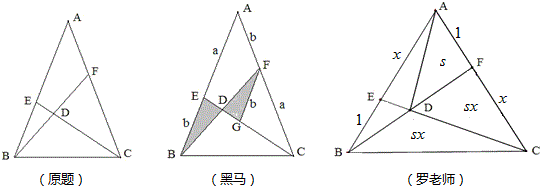
如图,已知△ABC中,AB=AC,AE=CF,BD=DF,求AE:AF 。
黑马的方法:
作FG∥AB,则 \dfrac{b}{a}=\dfrac{a}{a+b},得 \dfrac{a}{b}=\dfrac{1+\sqrt{5}}{2} 。
成都罗老师的方法:
设BE=1,AE=x,△ADF的面积为s,用面积法,\dfrac{s+sx}{sx}=\dfrac{x}{1},得 x=\dfrac{1+\sqrt{5}}{2} 。
陈宇欣的方法:
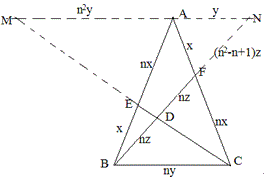
设AF=BE=x,AE=CF=nx,AN=y,BD=DF=nz,那么BC=ny,AM=n2y,
由△BCD∽△MND得FN=(n2-n+1)z,由△BCF∽△ANF得\dfrac{ny}{y}=\dfrac{2nz}{(n^2-n+1)z},
解得 n=\dfrac{1+\sqrt{5}}{2} 。
问题47(天津2012年中考题)
对于第(Ⅱ)题,春晓–团老师的解答:
∵y_0≥0,∴△≤0,即b2-4ac≤0,c\ge\dfrac{b^2}{4a}
黑马的解答:
问题48(2012/12/5黄伟建提供)
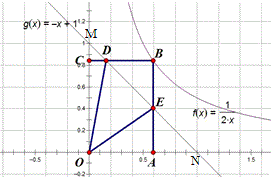
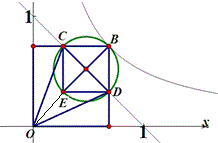
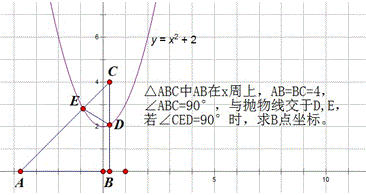
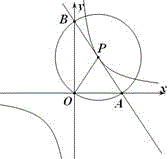
如图,B是双曲线y=\dfrac{1}{2x}第一象限上的动点,作BC⊥x轴,BA⊥y轴,交直线y=-x+1于D、E,求证:∠DOE=45°.
春晓——团老师解答:
黄伟建解答:
设B点坐标为(a,b)
∵CM=1-b=CD,AN=1-a=AE,BE=DB=a+b-1 ,
∴DE^2=MD^2+EN^2,将△OEN绕O点逆时针旋转90°可得证。
慈溪-徐浙峰的解法:
兴宁徐积国的解法是:
直线与x轴交为M,与y轴交于点N,△NOD相似于△MCO。
黑马指出:
这是以前的一个中考题,证明△MOE与△DNO相似,即可得45度。
慈溪李先兵补充证明相似的方法:
DN=\sqrt{2}y_B, EM=\sqrt{2}x_B, DN\cdot{EM}=2x_B\cdot{y_B}=1=OM\cdot{ON},
得△MOE∽△DNO,∠ODN=∠MOE,∠DOE=∠OMN=45°.
黑马又给出了一种方法:
问题49(2012/12/10黄伟建提供)
瑞安倪老师的解法:
黑马的解法:
问题50(春晓——团老师提供)
如图,矩形ABCD中,AD=6,AB=11,E,H,G,F分别在DC,AB,,BC,EH上,沿AE对折E落在F,沿EG对折C落在H,求DE的长。
江东单勤海的解答:
令DE=EF=x,EH=EC=11-x,易证AH=EH=11-x,FH=11-2x,在RT△AFH中用勾股定理就可以求x了。
问题51(2013/1/4)
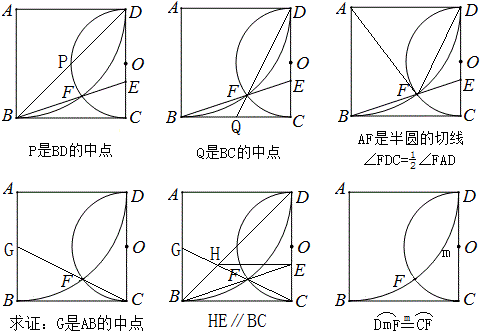
如图以矩形ABCD的顶点A为圆心、AB为半径的圆弧和以CD为直径的半圆交于F,直线BF交CD于E,求DE:EC的值。
古林中学张利芳解答:
由红蓝两个三角形相似,证得∠BDG=90°,∵∠BDC=45°,∴DC平分∠BDG,同样可得FE平分∠CFD,∴DE:EC=DF:FC=BD:DG=2:1.
黄伟建得出的一些结论:
黑马也得出了另一些结论:
问题52(北仑张阿水2013/1/5提供)
鲁玲莉解答:
问题53(单勤海自编)
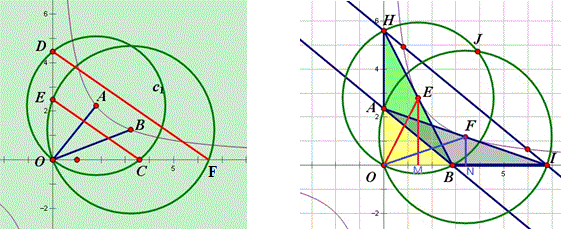
若任意的双曲线上任意两点A、B,分别连结AO,BO。以A、B为圆心,AO、BO为半径作圆,与坐标轴分别交于C、D、E、F,则CE//DF.
七中樊贞慧解答:
∵S△OEM=S△OFN,S△OHB=4S△OEM ,S△OIA=4S△OFN,∴S△OHB= S△OIA,
∴S△HAB= S△IAB,∴HI∥AB。
古林中学张利芳说:
单老师的结论还有:第一:EF平行上述两条直线,第二:梯形ABIH的中位线经过EF等等。
慈溪李先兵还找到了一个特例:
以双曲线上任意一点为圆心,以该点到原点的距离为半径作圆,交坐标轴的另两点记作A、B,则直线AB即为该点处的切线.
问题54(80中 –李东升2013年3月1日星期五提供)
七中樊贞慧解答:
问题55(萧山高磊提供)
萧山高磊解答:
m=1时,一个奇数;m=2时,两个奇数;m=3时,三个奇数,2013是第1007个奇数,此时m=?
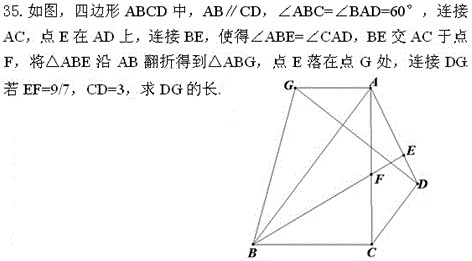
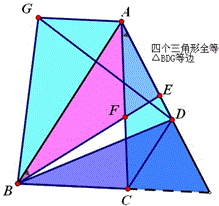
问题56(黄冈朱老师提供)
慈溪李先兵解答:
由∠CAD=∠ABE得△AEF∽△BEA,AE^2=EF\times{EB},因为AE=AG=CD=3,EF=\frac{9}{7},所以BE=7=BG=DG.
问题57(七中樊贞慧2013年3月2日提供)
锐角三角形ABC中,求证:2sinA>cosB+cosC.
黑马解答:
∵ A+B>90,A>90-B,∴sinA>cosB,同理sinA>cosBC,相加即可。
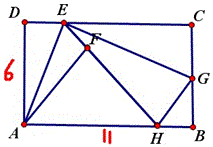
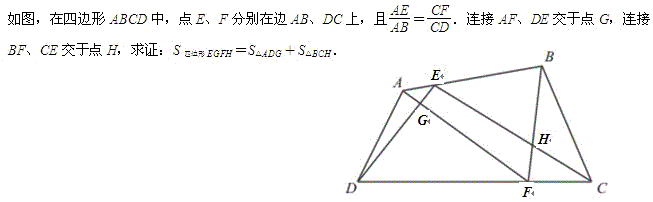
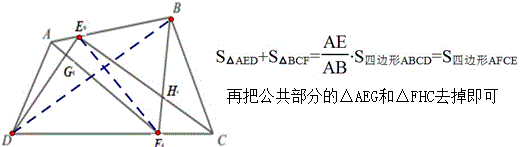
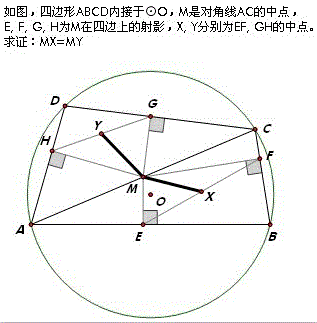
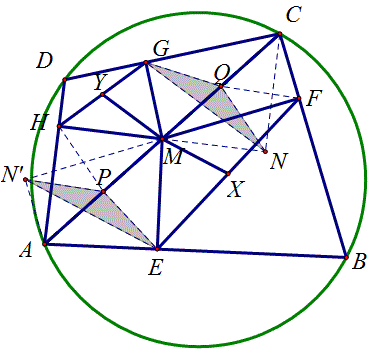
问题58(黑马2013年3月3日提供)
七中樊贞慧解答:
取AM,CM的中点P,Q,延长FM至N’使MN’=MF,延长HM至N使MN=MH,那么△MHP≌△MNQ,QN=HP=PM=AP=PE=QG,
同理,PN’=QF=QG,所以△QGN和△PEN’是腰长相等的等腰三角形。
因为M,N,F,C,G五点共圆,所以∠GQN=2∠GCN=2(∠DCA+∠DAC)=2(180°-∠D),
同理,A,N’,H,M,E五点共圆,所以∠EPN’=2∠EMN’=2(180°-∠FME)=2∠B,所以∠GQN=∠EPN’,
所以△GQN≌△EPN’,GQ=EN’,因为GQ=2MY,EN’=2MX,所以MX=MY.