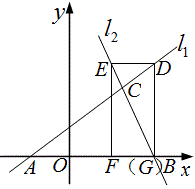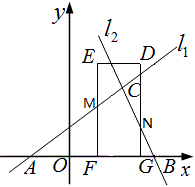本文是给学生看的,如果你是老师就跳过吧。
一、一次函数中特殊的k
已知直线y=kx+b
1、当k=±1时,直线与坐标轴交于45度的角;
2、当k=\pm\frac{\sqrt{3}}{3}或k=\pm\sqrt{3}时,直线与坐标轴交于30°或60°的角。
利用上述结论,可以使一次函数的许多问题简便许多。
二、列函数解析式(面积问题)
在列面积问题的函数解析式时,经常会遇到求特殊三角形的面积,下面是三种特殊三角形面积的计算公式。记住它们,有利于提高我们的计算速度。
1、边长为a的等边三角形面积:s=\frac{\sqrt{3}}{4}a^2;
2、较短直角边为a,含30°角的直角三角形面积:s=\frac{\sqrt{3}}{2}a^2;
3、较长直角边为a,含30°角的直角三角形面积:s=\frac{\sqrt{3}}{6}a^2。
例1 如图,已知直线l_1:y=\frac{\sqrt{3}}{3}x+\frac{4}{3}\sqrt{3}与直线l_2:y=-\sqrt{3}x+8\sqrt{3}相交于点C,分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线 上,顶点F,G都在x轴上,且点G与点B重合.
(1)求△ACB的面积;
(2)求矩形DEFG的边DG与DE的长;
(3)若矩形DEFG从B点出发,沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t秒,矩形DEFG与△ACB重叠部分的面积为s,求s关于t的函数关系式,并写出相应的t的取值范围.
解:(1)、(2)略。
(3)∵l_1:y=\frac{\sqrt{3}}{3}x+\frac{4}{3}\sqrt{3}中k=\frac{\sqrt{3}}{3},∴∠CAB=30°;
∵l_2:y=-\sqrt{3}x+8\sqrt{3}中k=-\sqrt{3},∴∠CAB=60°,所以l_1\perp{l_2}.
如图,当0≤t<3时,s=S△ABC-S△AFM-S△BNG,
∵BG=t,AF=8-t,∴S△BNG=\frac{\sqrt{3}}{2}t^2,S△AFM=\frac{\sqrt{3}}{6}(8-t)^2。
故s=18\sqrt{3}-\frac{\sqrt{3}}{2}t^2-\frac{\sqrt{3}}{6}(8-t)^2.
化简略,其它情形由读者完成。
三、二次根式的化简
1、约分
例2 解方程\sqrt{3}x+\sqrt{3}=x+3.
解:\sqrt{3}x-x=3-\sqrt{3},x=\frac{3-\sqrt{3}}{\sqrt{3}-1}=\frac{\sqrt{3}(\sqrt{3}-1)}{\sqrt{3}-1}=\sqrt{3}
2、提取
提取公因数来化简二次根式,往往比其它方法简单得多。
3、勾股数
利用特殊的勾股数可以较快地计算二次根式。
如3:4:5,5:12:13,1:\sqrt{3}:2,1:1:\sqrt{2},1:2:\sqrt{5},1:3:\sqrt{10}等等。
例3 计算\sqrt{39^2-36^2}
解:原式=\sqrt{3^2(13^2-12^2)}=3\times5=15.
很多人喜欢用平方差公式来化简,其实是麻烦的。
四、二次函数中的技巧
1、左同右异
这是用来判定y=ax^2+bx+c中b的符号,当对称轴在y轴左侧时a、b同号;当对称轴在y轴右侧时a、b异号。
2、对称性
抛物线是轴对称图形,利用对称性可以解决很多问题。如抛物线y=a(x-m)(x-n)对称轴是直线x=\frac{m+n}{2},又如抛物线y=a(x-1)^2+k过A(3,0),那么必过B(-1,0).
五、解方程的技巧
1、一元二次方程
约分是对任何方程化简的一种简便运算。
例4 解方程(4x-8)(3x+6)=96
解:12(x-2)(x+2)=96,x^2-4=8,x=\pm2\sqrt{3}
2、二元一次方程组
整体思想是一种技巧。
例5 已知\begin{cases} 2x + y = 8\\ x + 2y = 4 \end{cases},求x+y的值。
解:①+②得3x+3y=12,∴x+y=4.
六、有理数简便运算
有理数简便运算方法很多,现只举一例,即约分。
例6 已知抛物线y=169x^2-260x+676,求其顶点坐标。
解:x=-\dfrac{b}{2a}=\dfrac{260}{2\times169}=\dfrac{2\times13\times10}{2\times13\times13}=\dfrac{10}{13},
y=-\dfrac{4ac-b^2}{4a}=\dfrac{4\times169\times676-260^2}{4\times169}=\dfrac{2^2\times13^2\times676-2^2\times13^2\times10^2}{2^2\times13^2}=676-100=576,
故顶点坐标为(\dfrac{10}{13},576).
我们清楚看到,约分是初中数学各类运算中最最常用的手段,但现在的学生绝大多数不会约分,或者说想不到约分,这就是运算能力差的一个表现。
提高运算能力,从约分起步。