初中数学的核心有两个，一是运算，二是推理。运算的核心是字母表示数，而许多推理又离不开计算。
许多同学遇到稍难的题目，就想不到方法，其实首先想不到的是字母表示数。用字母解决数学问题有以下四个过程，有一个过程出问题就无法成功。
- 要想到设字母
- 要选择合适的未知数
- 列出有关的代数式
- 找出代数式之间的关系
下面举例说明。
例1 有一列按规律排列的数1，2，3，5，8，13，21，34，……。有一位同学说：这列数中任意相邻的6个数相加，我有简便运算的方法。请问简便运算的方法是怎样的？是如何发现的？
分析：我们不知道任意相邻的6个数是什么数，有些同学会用尝试的方法试试几个特殊的情况，就算得出结论，也只能算作猜想。如果设字母，就可以代表“任意”了。如果我们设任意相邻的6个数的第一个为a，那就无法表示其余5个数，也就是无法列代数式。我们可以继续设第二个数为b，这样这任意相邻的6个数可表示为a，b，a+b，a+2b，2a+3b，3a+5b，这6个数的和就是8a+12b。8a+12b=4(2a+3b)，这说明这6个数的和是第5个数的4倍。
上述解题方法完全符合“用字母解决数学问题的4个过程”，列表如下：
| 要想到设字母 | 如果设字母，就可以代表“任意”了 |
|---|---|
| 要选择合适的未知数 | 如果我们设任意相邻的6个数的第一个为a，那就无法表示其余5个数，也就是无法列代数式。我们可以继续设第二个数为b |
| 列出有关的代数式 | 这样这任意相邻的6个数可表示为a，b，a+b，a+2b，2a+3b，3a+5b，这6个数的和就是8a+12b |
| 找出代数式之间的关系 | 8a+12b=4(2a+3b)，这说明这6个数的和是第5个数的4倍 |
这种解题的思想就是代数思想，它是区别算术的主要标志。代数思想下面还有方程思想、函数思想、不等式思想、代数式思想，主要看你找到的关系是方程、函数、不等式还是代数式。而可以运用这种思想的题目非常多，可以是代数的，可以是几何的，可以是函数的，可以是三角的，还可以是统计的。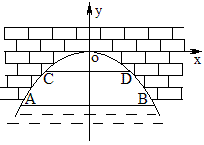
例2 有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米。
(1)在如图的坐标系中，求抛物线的表达式.
(2)若现在水面在CD处，洪水到来时，再持续多少小时才能到拱桥顶？(水位以每小时0.2米的速度上升)
分析：我们只就第1小题加以分析。由于抛物线的顶点是原点，故可设y=ax^2，但由于A、B、C、D四点都不知坐标，所以要引进字母。设B点坐标为（10,m)，那么D点坐标是(5,m+3)。将坐标代入后得：
\left\{\begin{matrix} 100a=m\\ 25a=m+3\end{matrix}\right.，解得a=-\frac{1}{25}
所以所求抛物线的解析式是y=-\frac{1}{25}x^2.
本题的解题思路又可以和“用字母解决数学问题的4个过程”对照如下：
| 要想到设字母 | 由于A、B、C、D四点都不知坐标，所以要引进字母 |
|---|---|
| 要选择合适的未知数 | 设B点坐标为（10,m) |
| 列出有关的代数式 | 那么D点坐标是(5,m+3) |
| 找出代数式之间的关系 | 将坐标代入后得\left\{\begin{matrix} 100a=m\\ 25a=m+3\end{matrix}\right. |
例3 施工队要维修一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米。现以O点为原点，OM所在直线为X轴建立直角坐标系（如图所示）。
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下。
分析：（1）M(12,0) ，P(6,6)（2）y=-\frac{1}{6}x^2+2x （3）要求AB、AD、DC的长度之和的最大值，就得设长度之和为L，自变量选择哪一个呢？如果设AB=x，就很难表示AD，如果设OB=x，就容易表示AB和AD。AB=CD=y=-\frac{1}{6}x^2+2x ，AD=12-2x，所以L=2（-\frac{1}{6}x^2+2x ）+（12-2x）=-\frac{1}{3}(x-3)^2+15，当x=3时，L_{max}=15。
第3小题分析思路和4个基本思考过程对照如下：
| 要想到设字母 | 要求AB、AD、DC的长度之和的最大值，就得设长度之和为L，自变量选择哪一个呢 |
|---|---|
| 要选择合适的未知数 | 如果设AB=x，就很难表示AD，如果设OB=x，就容易表示AB和AD |
| 列出有关的代数式 | AB=CD=y=-\frac{1}{6}x^2+2x ，AD=12-2x |
| 找出代数式之间的关系 | L=2（-\frac{1}{6}x^2+2x ）+（12-2x）=-\frac{1}{3}(x-3)^2+15 |
例4 在采石场进行爆破作业时，点燃导火索后马上离开，距离爆破点100m以外就安全了。人离开的速度为2m/s，导火索燃烧的速度是5cm/s，问导火索的长度至少多少m？（精确到0.01米）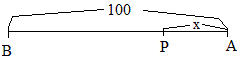
分析：如图，A为爆破点，AP为导火索，P为点燃点，B为安全区，设PA=xm，那么PB=(100-x)m，人离开的时间为\frac{100-x}{2}s，导火索燃烧的时间为\frac{x}{0.05}s，于是\frac{100-x}{2}\le\frac{x}{0.05}，解得x\ge\frac{100}{41}\approx2.44，即导火索长度至少为2.44m。
本题分析思路和4个基本思考过程对照如下：
| 要想到设字母 | 任何人一定能想到这一步 |
|---|---|
| 要选择合适的未知数 | 设PA=xm |
| 列出有关的代数式 | PB=(100-x)m，人离开的时间为\frac{100-x}{2}s，导火索燃烧的时间为\frac{x}{0.05}s |
| 找出代数式之间的关系 | 于是\frac{100-x}{2}\le\frac{x}{0.05}，解得x\ge\frac{100}{41}\approx2.44 |
上面4例中都是代数问题，找出的关系有代数式的，有方程的，有函数的还有不等式的，下面举例说明代数思想在几何中的应用。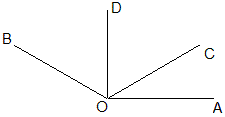
例5 如图，射线OC、OD在∠AOB的内部，∠AOC=\frac{1}{5}∠AOB，OD平分∠BOC，∠BOD与∠AOC互余，求∠AOB的度数．
分析：这个问题中每一个锐角都未知，所以要想到设字母。因为所有的角都以∠AOC作为基础，所以可以设∠AOC=x^\circ，则∠BOD=(\frac{5x-x}{2})^\circ。于是有\frac{5x-x}{2}+x=90，解之x=30，所以∠AOB=30×5=150^\circ。
本题分析思路和4个基本思考过程对照如下：
| 要想到设字母 | 这个问题中每一个锐角都未知，所以要想到设字母 |
|---|---|
| 要选择合适的未知数 | 因为所有的角都以∠AOC作为基础，所以可以设∠AOC=x^\circ |
| 列出有关的代数式 | 则∠BOD=(\frac{5x-x}{2})^\circ |
| 找出代数式之间的关系 | 于是有\frac{5x-x}{2}+x=90，解之x=30 |
例6 如图，△ABC中，AC=BC=5，AB=6，矩形DEFG是△ABC的内接矩形，当EG//BC时，求矩形DEFG的面积。
分析：本题中若不考虑EG//BC的条件，那么图中的许多线段是变量，其中一条确定了，其余也随之确定。于是应该设其中某条线段为x。用什么方法来建立关系呢？方法很多，如找相似三角形建立比例式的关系，也可以找直角三角形建立勾股定理的关系，也可以找等腰三角形建立三线合一的关系，等等。经过尝试，后者最为简便，即证明△GAE为等腰三角形，于是设AD为x容易表示其它线段，所以DE=6-2x，因为AD=DE，故x=6-2x，x=2。接下去的问题就不难了。
本题分析思路和4个基本思考过程对照如下：
| 要想到设字母 | 本题中若不考虑EG//BC的条件，那么图中的许多线段是变量，其中一条确定了，其余也随之确定。于是应该设其中某条线段为x |
|---|---|
| 要选择合适的未知数 | 用什么方法来建立关系呢？方法很多，如找相似三角形建立比例式的关系，也可以找直角三角形建立勾股定理的关系，也可以找等腰三角形建立三线合一的关系，等等。经过尝试，后者最为简便，即证明△GAE为等腰三角形，于是设AD为x容易表示其它线段 |
| 列出有关的代数式 | 所以DE=6-2x |
| 找出代数式之间的关系 | 因为AD=DE，故x=6-2x，x=2 |
本例难在找关系，很多学生做这道题都困于关系找得复杂而解不出结果。常常越简单的关系越难以发现，所以要多想几种方法，才能比较得出更加合理的做法。
字母表示数自初一第一册开始学习，但到了初三还有好多学生想不到用。如上面的例1，我在我的班级里试了一下，结果能想到用字母解决问题的人不到一半，能想到用2个字母的人不到三分之一，能列出6个数和的代数式就更少，最后能找出4倍关系的并能说明理由的只有2人了。现在的学生让他计算现成的式子、解已有的方程或不等式都不会有什么困难，但要他主动想到代数思想的4个基本过程，把它作为一种工具来使用，那就很困难了。
为了让同学们有更多练习的机会，下面又为你准备了一些题，解这些题仍然离不开这“4个过程”，亲爱的你不妨一试。
练习1 小明和小慧玩猜数游戏，小明说：“你心里想一个数，把它乘以6，减去3，所得的差除以3，再加上你想的数。只要你告诉我正确的结果，我就可以猜出你心里想的是什么数”。
小慧很好奇，告诉小明自己的计算结果是-2，心里想：小明真的能猜到自己想的数吗？
（1）小明能猜到小慧想的数是几？
（2）小明为何总能猜到别人（不一定是小慧）心里想的数？猜数的方法是什么？
（3）请你也设计一个游戏，规则是：让对方心里想一个数，你规定运算方法进行计算，你能猜出他的结果。
练习2 已知点A、B在双曲线y=\frac{4}{x}上，C、D在x轴上，△OAC和△CBD是等腰直角三角形，求D点的坐标。
练习3 如果一个正整数能表示为两个连续偶数的平分差，那么称这个正整数为“神秘数”．如：4=2^2-0^2，12=4^2-2^2，20=6^2-4^2。因此4，12，20都是“神秘数”。
（1）28和2012这两个数是“神秘数”吗？为什么？
（2）“神秘数”具有什么特点？
（3）两个连续奇数的平方差（取正数）是“神秘数”吗？为什么？
练习4 已知锐角\alpha与\beta互补，那么下列语句正确的是（ ）
A.\alpha的余角和\beta补角互余 B.\alpha的余角和\beta补角互补
C.\alpha的补角和\beta余角互余 D.\alpha的补角和\beta余角互补
练习5 半导体收音机的电路板是用铜箔放在稀盐酸中进行化学腐蚀制成的。工艺规定：腐蚀槽里纯盐酸的含量低于48克或高于96克，均不能进行化学腐蚀。现在腐蚀槽里已经有18克的纯盐酸，工作时机器每分钟自动向腐蚀槽里注入6克纯盐酸。实验测定在规定的浓度下腐蚀8分钟为有效，少于或多于这个时间为无效。请问按这样规定，腐蚀工作是否有效？为什么？
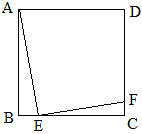练习6 如图，正方形ABCD中，动点E在线段BC上移动(不与B，C重合)，连接AE，过点E作EF⊥AE，交边CD于点F， E点运动时，F点能否到达CD的中点？请说明理由。
练习7 如图，在等腰直角三角形ABC中，D是斜边AB上的一个动点，E为BC上的一点，且DC=DE，EF⊥AB,垂足为点F. AC=2。求证：DF=\frac{1}{2}AB。
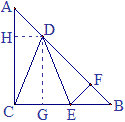提示：作矩形CGDH，设AH=x，那么就可以用x表示AD、BF，因为AB=AB=2\sqrt{2}，于是可以进一步表示DF，你会发现DF=AB=\sqrt{2}，从而DF=\frac{1}{2}AB。
这种方法我称之为“计算法”，即通过对某些几何元素（线段或角）的代数计算，而达到证明数量关系的目的。