没想到才过4天,一道几何作图题征集到多人的解答,并在QQ群(出众树雪88730268)上引起大讨论,看来数学研究就得这样,有问题大家研究,有结果大家分享。
一、问题提出
问题1
一位老师问我:在一个长8厘米、宽6厘米的长方形内画两个圆,这两个圆的面积之和最大是多少?
因为百思不得其解,于是想用几何画板绘制图形,以探索最大值的位置。但作图遇到了困难,也就是
问题2
如图在已经画出矩形ABCD和圆P后怎样用尺规作出圆Q。
其实,为了解决问题1,这样的作图是错误的,在最后我们再谈这个问题。
二、问题探索
曾经我解决过这样一个作图题:
问题3
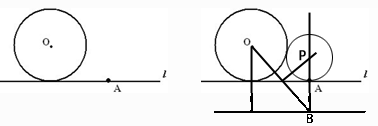
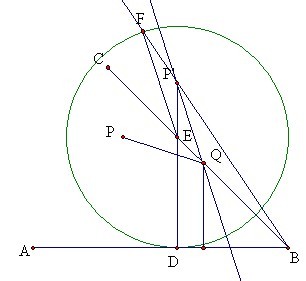
如图,已知圆O和直线l上一点A,求作圆P,使圆P与圆O外切,且与直线l相切于A。
作法是:在过点A的l垂线上截取AB等于圆O半径r,作OB的中垂线交这条垂线于P,P即为所求的圆心。(这个方法想得我好辛苦)
我这里的想法是要在过A点l的垂线上找一点P,使PO-r=PA,如何改造这个条件,使P到两个定点的距离相等呢?于是想到了B点,有PB=PO。
受到这个作图的启发,我对上述问题有了新的思路:
如图,将AB往下平移圆P半径R的距离,过B点作∠A’B’C’=45°。于是就产生了
问题4
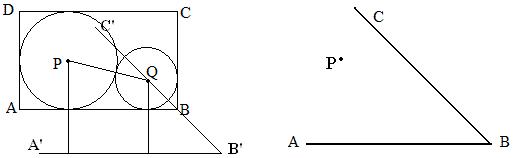
∠ABC=45°,P为角内部的一个定点,用尺规在射线BC上找一点Q,使Q到AB的距离等于QP。
三、问题解决
对于问题2和问题4我请教了同行,以下是同行的解答。
对于问题2,李玉荣老师在凤凰数学论坛中给出了一种结合代数方法的解答:
如图,设大圆与AB切于E,BE=a,大圆半径为R,小圆半径为r,
可以得到方程(R+r)^2=(R-r)^2+(a-r)^2,
解得r=a+2R-2\sqrt{R(a+R)},
由射影定理可作出线段\sqrt{R(a+R)},
进而可作出r=a+2R-2\sqrt{R(a+R)}。
对问题2宁波市曙光中学胡伟斌老师也给出了结合代数的解法:
如上图,大圆半径为b,AB=a,同样可以列出方程
(b+r)^2=(b-r)^2+(a-b-r)^2,
解得r=a+b-2\sqrt{ab},接下来的方法还是用射影定理。
对于问题4,宁波市海曙区教研员高友军老师是这样解的:
1、作点P关于直线BC的对称点P’;
2、作射线B P’;作P’D⊥AB于D,交BC于E;
3、在B P’上截取一点F,使EF=ED;
4、过P’作P’Q∥EF交BC于Q.
这样可以作QH⊥AB于H,然后证明DE:QH=EF:P’Q,从而得到P’Q= QH=QP。
值得一提的是,高老师的方法实在很难想到,实在太妙了,高老师是高手啊。
我对问题4的解决方法:
1、作PD⊥AB;
2、作PD的中垂线,垂足为E;
3、作矩形,使其宽为2PE,长为PE+EF(F在BC上);
4、作最大的圆P和最大的圆Q(作圆Q的方法见上)
结论:点Q就是所求。
追加:
2011年4月7日,宁波邱隘实验中学马昌敏老师传过来他最新最好的解法:
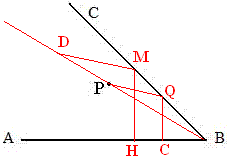
如图,作射线BP,在射线BC上任取一点M,作MH⊥AB于H,在BP上截取D点,使MD=MH,过P作PQ∥DM交BC于Q,点Q即为所求。
四、问题思考
思考1
按照高友军老师的作图方法,可知不论∠ABC等于几度,只要P在角内部,点F必有2个,故点Q必有2解。
思考2
为什么我对问题4的解决方法里,只能作出1个解呢?正在思考中……
思考3 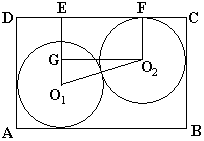
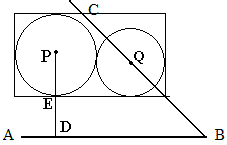
我原来的想法都不能解决问题1.因为问题1要求两个圆面积和最大,两圆应该放在相对的位置(如图)。
设圆O_1的半径为x,圆O_2的半径为m,则有
(6-x-m)^2+(8-x-m)^2=(x+m)^2,
即(x+m)^2-28(x+m)+100=0,解得m=14-4\sqrt{6}-x,
∴两圆面积和=\pi[x^2+(14-4\sqrt{6}-x)^2]
=\pi[2x^2-2(14-4\sqrt{6})x+(14-4\sqrt{6})^2
=2\pi[(x-(7-2\sqrt{6})]^2+2\pi(7-2\sqrt{6})^2
可见,当x=7-2\sqrt{6}时,
面积和最小值=2\pi(7-2\sqrt{6})^2。
这时两个圆是等圆!这个结论的前提是两圆及矩形之间要相切。
那么面积和的最大值是多少呢?由上面推导可得两圆半径之和为定值,即m+x=14-4\sqrt{6},继而可得m和x的差最大时,面积和最大(即问题2)。
追加:
宁波邱隘实验中学马昌敏老师对最大值的问题给出了完整的解答:
由上可知,设圆O_1的半径为x,圆O_2的半径为m,则有
m+x=14-4\sqrt{6},且11-4\sqrt{6}\le{x}\le{3},
当x=3或x=11-4\sqrt{6}时,两圆面积之和取得最大值。最大值是
\pi[(11-4\sqrt{6})^2+3^2]=\pi(226-88\sqrt{6})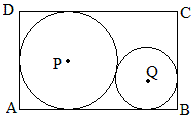
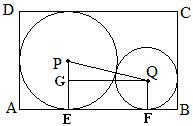
@小张
小张,你这个QQ93966732,是黑龙江的,不让加好友耶,你确认号码没错?
我已经写好求最大值的过程,符号不会打,最大值为配(226-88根号6),此问题无最小值,若要过程,可以联系我:QQ 93966732(马)
此问题面积的和无最小值!
高老师所言甚是,已经做了改正。谢谢高老师。
要使面积和最大,两圆及矩形之间要相切。从而可得两圆半径之和为定值,继而可得差最大时,面积和最小(即问题2)
实际求的好像是和的最小值唉